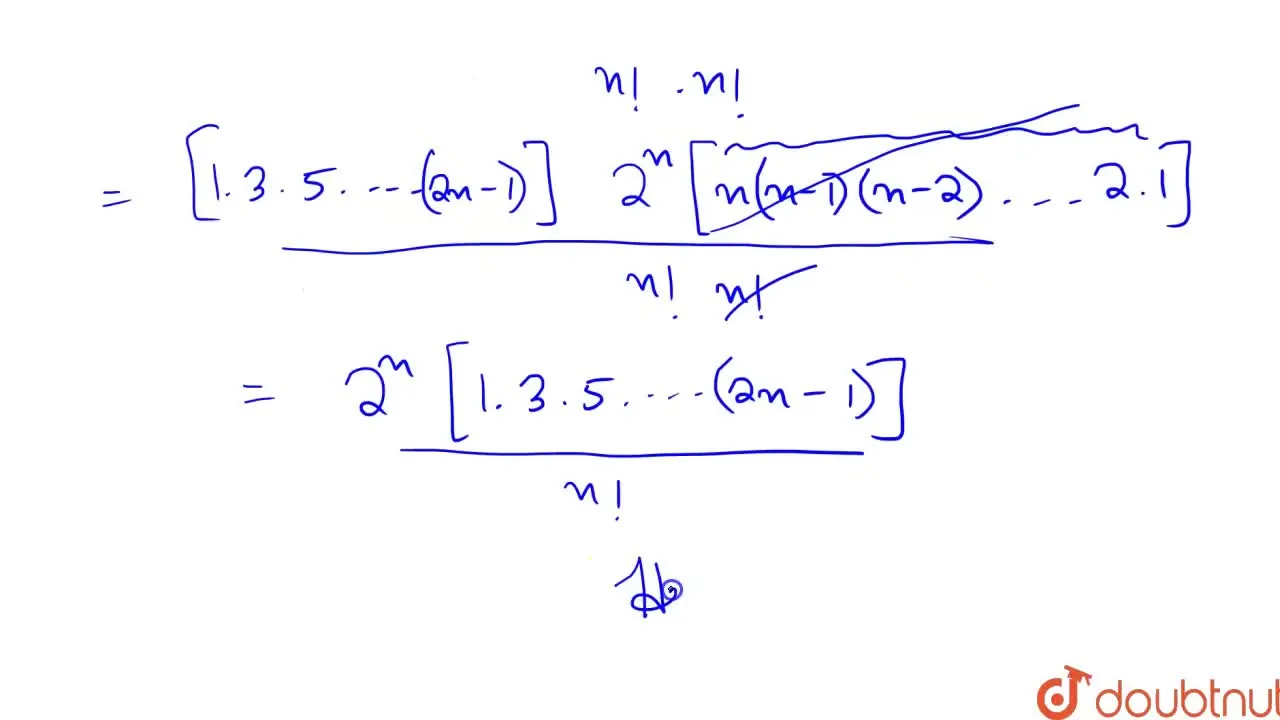Prove that .2nCn=2n×[1⋅3⋅5...(2n−1)]n!.
Video Solution
Text Solution
.1nCn=(2n)!(n!)(2n−n)!=(2n)!(n!)2
=(2n)(2n−1)(2n−2)...4⋅3⋅2⋅1(n!)2
=[(2n)(2n−2)(2n−4)...4⋅2]×[(2n−1)(2n−3)...5⋅3⋅1](n!)2
=2n[n(n−1)(n−2)...2⋅1]×[(2n−1)(2n−3)...5⋅3⋅1](n!)2
=2n×(n!)×[1⋅3⋅5...(2n−3)(2n−1)](n!)2
=2n×[1⋅3⋅5...(2n−3)(2n−1)](n!).
Hence, .2nCn=2n×{1×3×5×...×(2n−1)}n!.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Practical Problems on Combinations (Solved Examples)25videos
COMBINATIONS
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Mixed Problems on Permutations and combinations (Solved Examples)5videos
COMBINATIONS
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D18videos
COMBINATIONS
- BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 B18videos
CIRCLE
- BOOK - RS AGGARWALCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5 G28videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
Similar Questions
Prove that: 2n!n!=(2n[1.3.5(2n−1)])
View SolutionProve that (2n+1)!n!=2n[1.3.5.....(2n−1).(2n+1)]
View SolutionProve that (4n)C2n(2n)Cn=1.3.5....(4n−1)[1.3.5...(2n−1)]2
View SolutionProve that (2n)!n!=2n×{1×3×5×...×(2n−1)}.
View SolutionProve that (2n)!n!=2n{1.3.5(2n−1)}
View SolutionProve that: (2n)!n!={1.3.5(2n−1)}2n.
View SolutionProve that nC2n0Cn−nC2n−11Cn+nC2×2n−2Cn++(−1)n^nCnnCn=1.
View SolutionProve that ^nC2n0Cn−nC2n−21Cn+nC2n−42Cn=2n.
View SolutionProve that: ^(2n)C0−3.2nC1+32.2nC2−..+(−1)2n..32n^(2n)C2n=4n for all value of N
View SolutionProve that C20+C21+...C2n=2n!n!n!
View Solution