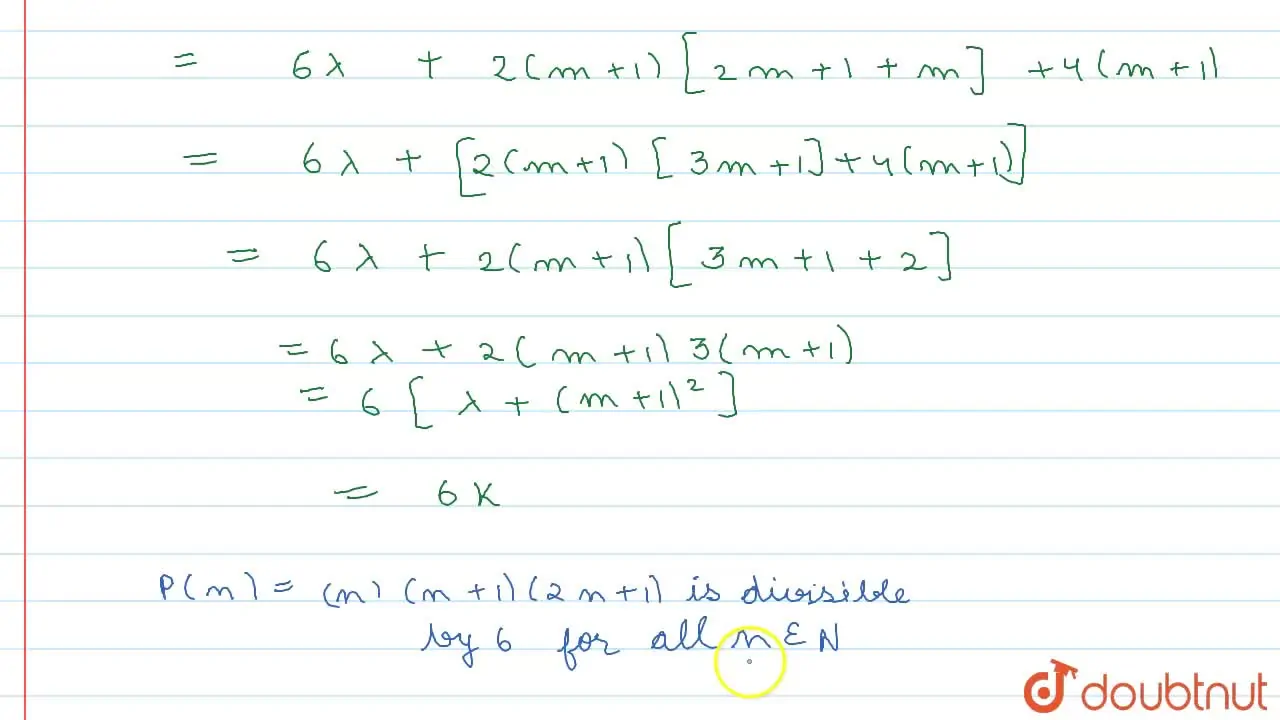Prove by the principle of mathematical induction that: n(n+1)(2n+1) is divisible by 6 for all n∈N.
Step by step video & image solution for Prove by the principle of mathematical induction that: n(n+1)(2n+1) is divisible by 6 for all n in Ndot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
Prove the following by the principle of mathematical induction: 52n−1 is divisible by 24 for all n∈N.
View SolutionProve by the principle of mathematical induction that n<2nfor alln∈N.
View SolutionUsing the principle of mathematical induction, prove that (23n−1) is divisible by 7 for all n∈N.
View SolutionUsing the principle of mathematical induction, prove that (23n−1) is divisible by 7 for all n∈N.
View SolutionUsing the principle of mathematical induction, prove that (23n−1) is divisible by 7 for all n∈N.
View SolutionProve the following by the principle of mathematical induction: x2n−1+y2n−1 is divisible by x+y for all n∈N.
View SolutionProve the following by the principle of mathematical induction: 32n+7 is divisible by 8 for all n∈N.
View SolutionUsing the principle of mathematical induction, prove that (23n−1) is divisible by 7 for all n∈N
View SolutionUsing the principle of mathematical induction, prove that (23n−1) is divisible by 7 for all n∈N
View SolutionProve by the principle of mathematical induction that 2n>n for all n∈N.
View Solution