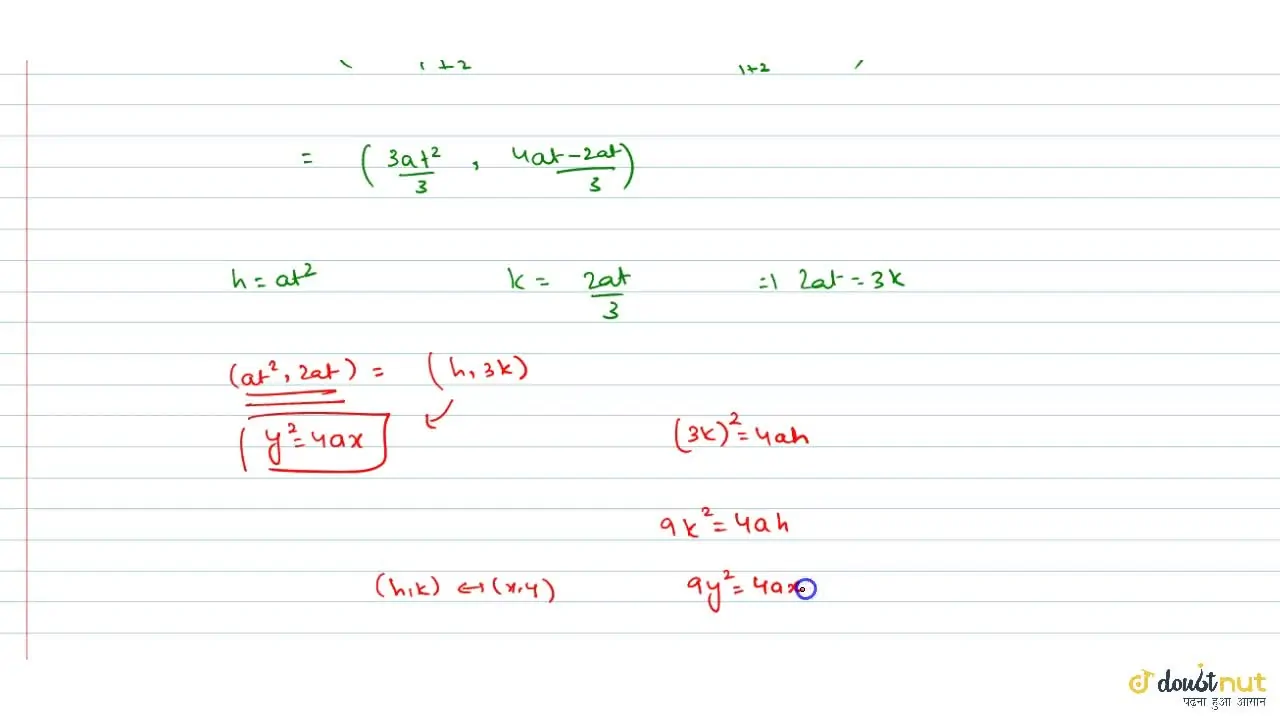PQ is a double ordinate of a parabola y2=4ax. Find the locus of its points of trisection.
For the parabola y2=4ax we have,
x=at2,y=2at.
So, we can consider point P(at2,2at) and Q(at2,−2at), then its points of trisection have ordinates y1 and y2 where:
y1=−2at+4at3=2at3
y2=−4at+2at3=−2at3
For both of these points,
y2=4a2t29
y2=(4a9)(at2)
y2=49ax, which is the required locus of the trisection.
Related Playlists
Similar Questions
PQ is a double ordinate of a parabola y2=4ax. Find the locus of its points of trisection.
View SolutionPQ is a double ordinate of a parabola y2=4ax. Find the locus of its points of trisection.
View SolutionPQ is a double ordinate of a parabola y2=4ax. The locus of its points of trisection is another parabola length of whose latus rectum is k times the length of the latus rectum of the given parabola, the value of k is
View SolutionPQ is a double ordinate of the parabola y2=4ax. If the normal at P intersect the line passing through Q and parallel to axis of x at G, then locus of G is a parabola with -
View SolutionIf latus rectum of ellipse x225+y216=1 is double ordinate of parabola y2=4ax, then find the value of a.
View SolutionIf the line lx+my+n=0 is a tangent to the parabola y2=4ax , then locus of its point of contact is:
View SolutionThe ordinates of points P and Q on the parabola y2=12x are in the ration 1:2 . Find the locus of the point of intersection of the normals to the parabola at P and Q.
View SolutionPQ is a focal chord of the parabola y2=4ax,O is the origin. Find the coordinates of the centroid. G. of triangle OPQ and hence find the locus of G as PQ varies.
View SolutionLet PQ be a double ordinate of the parabola, y2=−4x where P lies in the second quadrant. If R divides PQ in the ratio 2:1 then teh locus of R is
View SolutionA variable chord of the parabola y2=8x touches the parabola y2=2x. The the locus of the point of intersection of the tangent at the end of the chord is a parabola. Find its latus rectum.
View Solution