Parallel lines
Step by step video, text & image solution for Parallel lines by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Similar Questions
Two non - parallel line segments will always intersect.
View SolutionTwo transversals S and T cut a set of distinct parallel lines. S cuts the parallel lines in points A, B, C, D and T cuts the parallel lines in points E,F, G and H, respectivley. If AB = 4, CD = 3 and EF = 12, then what is the length of GH ?
View SolutionTwo transversals S and T cut a set of distinct parallel lines. S cuts the parallel lines in points A,B,C and D and T cuts the parallel lines in points E,F,G,H repectively. If AB = 4, CD = 3 and EF = 12, then what is length of GH ?
View SolutionIdentify parallel line segments in each of the figures given below :
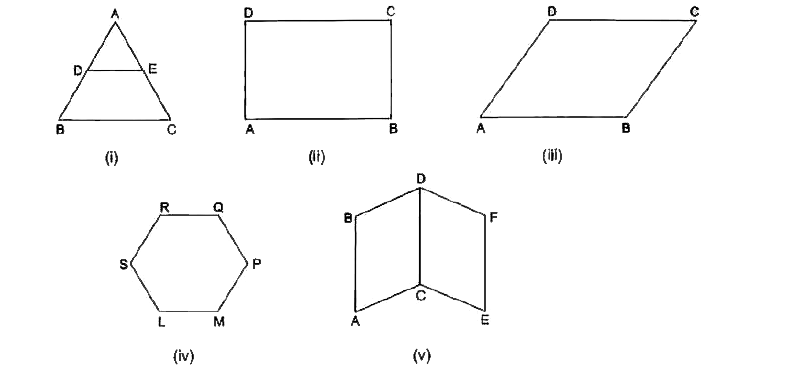 View Solution
View SolutionWhich of the following statements are true (T) and which are false (F)? Give reasons. (i)If two lines are intersected by a transversal, then corresponding angles are equal. (ii)If two parallel lines are intersected by a transversal, then alternate interior angles are equal. (iii)Two lines perpendicular to the same line are perpendicular to each other. (iv)Two lines parallel to the same line are parallel to each other. (v)If two parallel lines are intersected by a transversal, then the interior angle on the same side of the transversal are equal.
View SolutionChecking For Parallels Lines|Questions Practice|OMR
View SolutionNo. of square rectangle parallelogram formed when m parallel & n parallel line intersect
View SolutionNormal Form OF Line||Angle Between Line || Parallel and Perpendicular Lines
View SolutionIf 5 parallel straight lines are intersected by 4 parallel straight lines, then find the number of parallelograms thus formed.
View SolutionCondition of parallel and perpendicular lines
View Solution


