P, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
To prove that quadrilateral PQRS is a rhombus, we need to show that its opposite sides are equal in length and that its diagonals bisect each other at right angles. Given that P, Q, R, and S are the midpoints of sides AB, BC, CD, and DA of quadrilateral ABCD, and that AC = BD, we can follow these steps:
1. Identify Midpoints:
Let P, Q, R, and S be the midpoints of sides AB, BC, CD, and DA respectively.
2. Use the Midpoint Theorem:
According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long.
3. Apply the Midpoint Theorem to Triangles:
- In triangle ABC, P and Q are midpoints of AB and BC respectively. Therefore, segment PQ is parallel to AC and PQ = 1/2 * AC.
- In triangle ADC, S and R are midpoints of DA and CD respectively. Therefore, segment SR is parallel to AC and SR = 1/2 * AC.
- Since AC = BD (given), we can also say that SR = 1/2 * BD.
4. Establish Parallel Sides:
- From the above, we have PQ || SR and PQ = SR.
- Similarly, in triangle ABD, P and S are midpoints of AB and DA respectively. Therefore, segment PS is parallel to BD and PS = 1/2 * BD.
- In triangle BCD, Q and R are midpoints of BC and CD respectively. Therefore, segment QR is parallel to BD and QR = 1/2 * BD.
5. Establish Equality of Opposite Sides:
- From the above, we have PS || QR and PS = QR.
- We have established that PQ = SR and PS = QR.
6. Conclude that PQRS is a Rhombus:
- Since opposite sides are equal (PQ = SR and PS = QR) and parallel (PQ || SR and PS || QR), quadrilateral PQRS is a rhombus.
Let P, Q, R, and S be the midpoints of sides AB, BC, CD, and DA respectively.
According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long.
- In triangle ABC, P and Q are midpoints of AB and BC respectively. Therefore, segment PQ is parallel to AC and PQ = 1/2 * AC.
- In triangle ADC, S and R are midpoints of DA and CD respectively. Therefore, segment SR is parallel to AC and SR = 1/2 * AC.
- Since AC = BD (given), we can also say that SR = 1/2 * BD.
- From the above, we have PQ || SR and PQ = SR.
- Similarly, in triangle ABD, P and S are midpoints of AB and DA respectively. Therefore, segment PS is parallel to BD and PS = 1/2 * BD.
- In triangle BCD, Q and R are midpoints of BC and CD respectively. Therefore, segment QR is parallel to BD and QR = 1/2 * BD.
- From the above, we have PS || QR and PS = QR.
- We have established that PQ = SR and PS = QR.
- Since opposite sides are equal (PQ = SR and PS = QR) and parallel (PQ || SR and PS || QR), quadrilateral PQRS is a rhombus.
Topper's Solved these Questions
Similar Questions
Knowledge Check
M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB+AD+CB+CD is equal to
A2 MNB2NMC4 MND4 NM
Let P, Q, R, S be respectively the midpoints of the sides AB, BC, CD and DA of quad. ABCD Show that PQRS is a parallelogram such that
ar(||gm PQRS)=12ar(quad. ABCD).
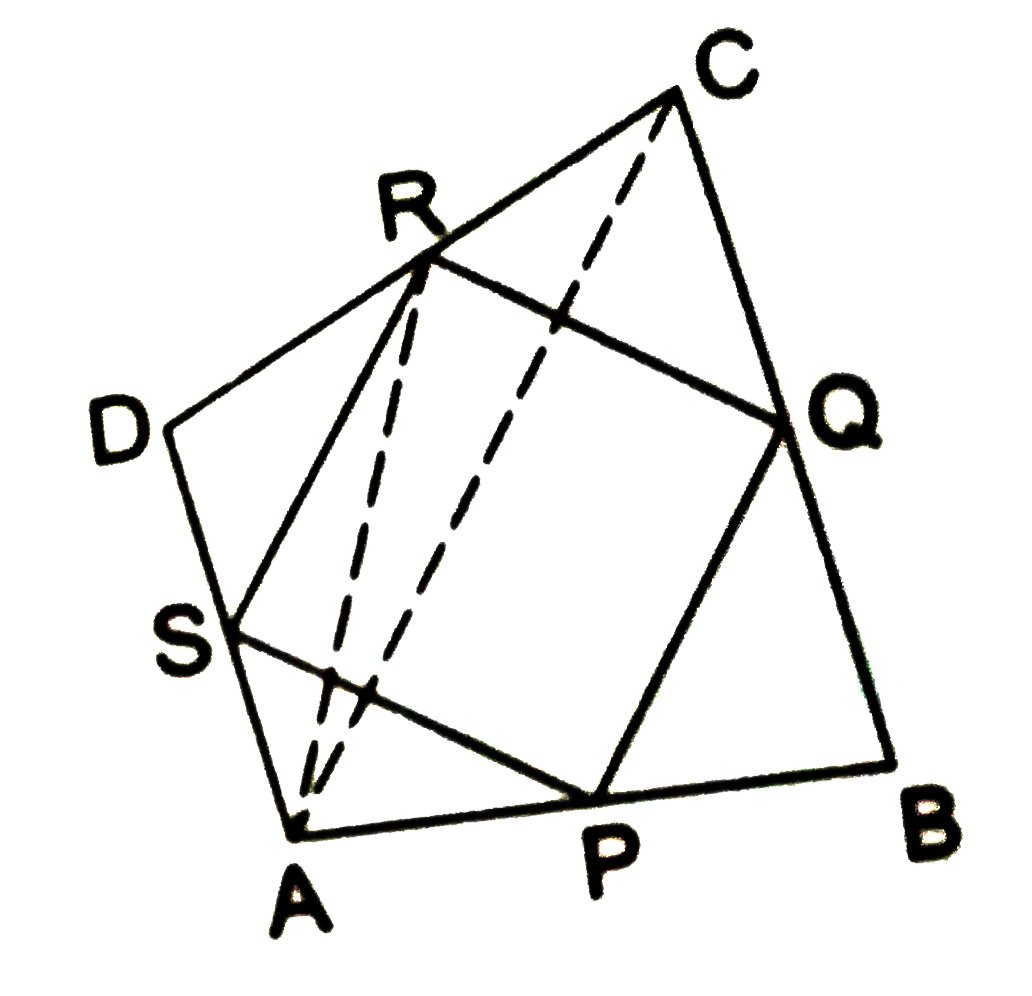
View SolutionP, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that
ar(|| gm PQRS)=12×ar(∣∣gmABCD).
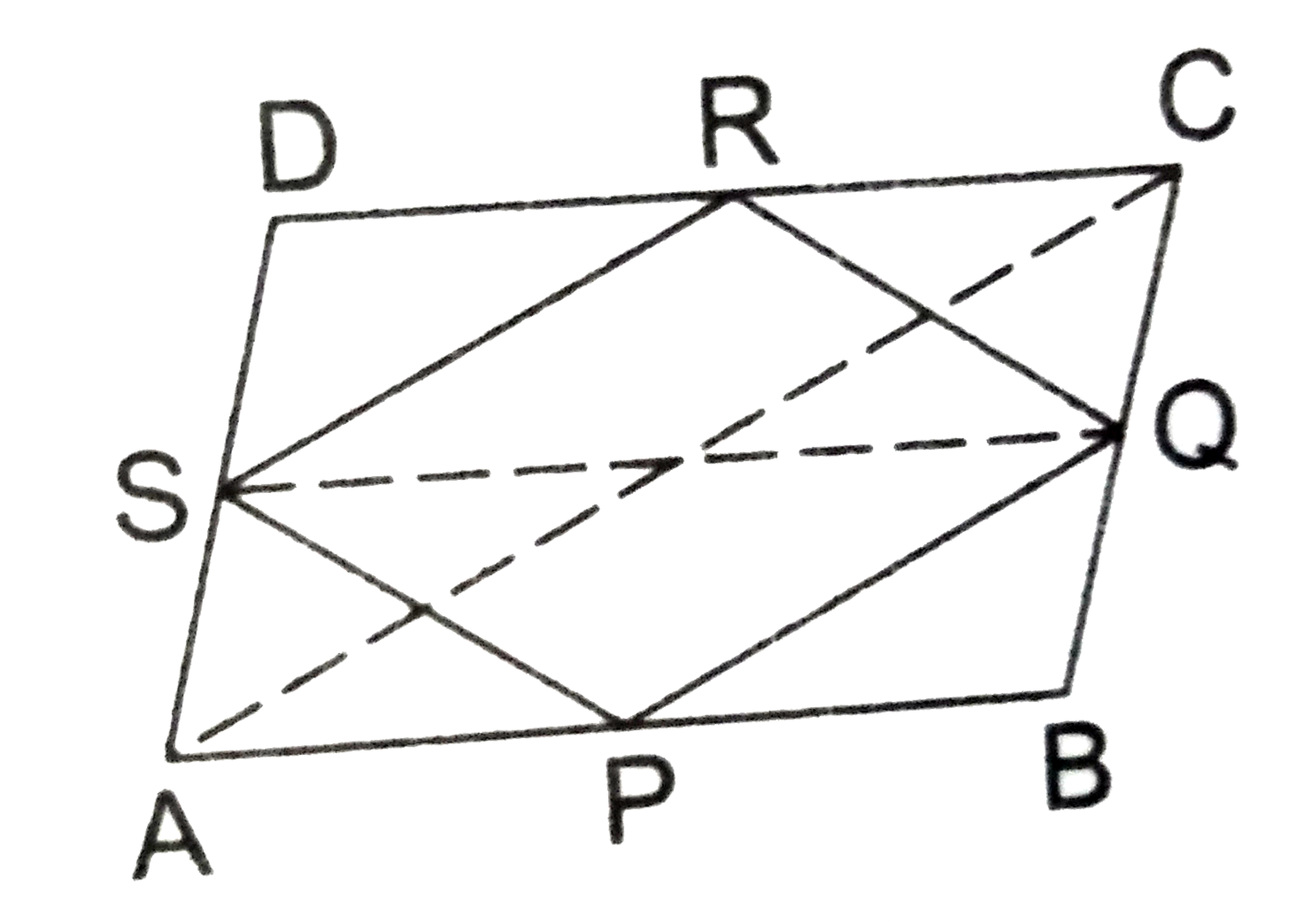
View SolutionK, L, M and N are points on the sides AB, BC, CD and DA respectively of a square ABCD such that AK = BL = CM = DN. Prove that KLMN is a square.
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.
View Solution

