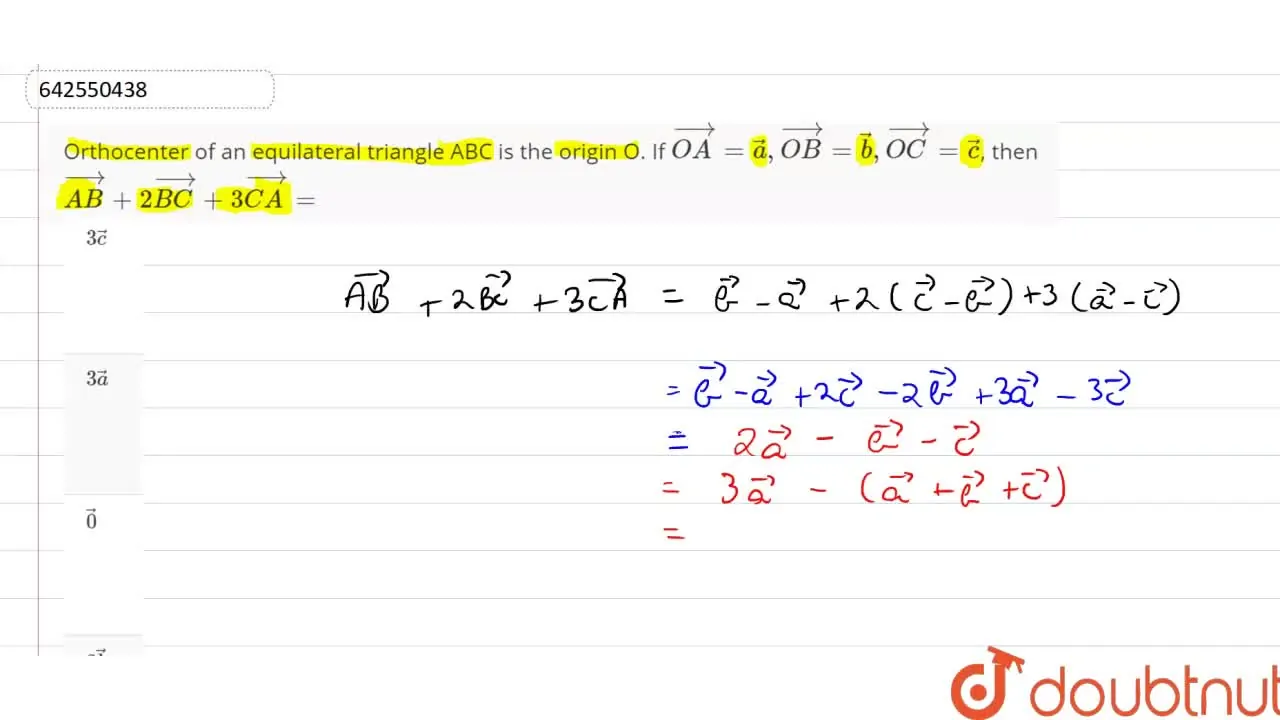
Orthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
3→c
3→a
→0
3→b
The correct Answer is:B
For an equilateral triangle, centroid is the same as orthocenter
∴−−→OA+−−→OB+−−→OC3=→0
∴−−→OA+−−→OB+−−→OC=→0
Now, −−→AB+2−−→BC+3−−→CA
=−−→OB−−−→OA+2−−→OC−2−−→OB+3−−→OA−3−−→OC
=−−−→OB+2−−→OA−−−→OC
=−(−−→OB+−−→OA+−−→OC)+3−−→OA
=3−−→OA
=3→a
Related Playlists
Similar Questions
If ∣∣∣−−→AO+−−→OB∣∣∣=∣∣∣−−→BO+−−→OC∣∣∣ , then A,B,C form
View SolutionAssertion ABCDEF is a regular hexagon and −−→AB=→a,−−→BC=→band−−→CD=→c,then−−→EA is equal to −(→b+→c), Reason: −−→AE=−−→BD=−−→BC+−−→CD (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not te correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionLet O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SGView SolutionLet O be the centre of the regular hexagon ABCDEF then find −−→OA+−−→OB+−−→OD+−−→OC+−−→OE+−−→OF
View SolutionIf ABCDEF is a regular hexagon with −−→AB=→a and −−→BC=→b, then −−→CE equals
View SolutionIn a triangle OAC, if B is the mid point of side AC and →OA=→a, →OB=→b, then what is →OC?
View SolutionProve that 3−−→OD+−−→DA+−−→DB+−−→DC is equal to −−→OA+−−→OB+−−→OC.
View SolutionIn triangle ABC (Figure), which of the following is not true:
(A)−−→AB+−−→BC+−−→CA=→0
(B)−−→AB+−−→BC−−−→AC=→0
(C)−−→AB+−−→BC−−−→CA=→0
(D)−−→AB+−−→CB+−−→CA=→0
 View Solution
View SolutionLet O be the centre of a regular pentagon ABCDE and −−→OA=→a, then −−→AB+−−−→2BC+−−−→3CD+−−−→4DE+−−−→5EA is equals:
View SolutionLet O be the centre of a regular pentagon ABCDE and −−→OA=→a, then −−→AB+−−−→2BC+−−−→3CD+−−−→4DE+−−−→5EA is equals:
View Solution