On the set R−{−1} a binary operation ⋅ is defined by a⋅b=a+b+ab for all a,b∈R−1{−1} . Prove that * is commutative as well as associative on R−{−1}. Find the identity element and prove that every element of R−{−1} is invertible.
We have
a⋅b=a+b+ab for all a,b∈A, where A=R−{−1}
Commutativity: For any a,b∈R−{−1}
To prove:a⋅b=b⋅a
Now, a⋅b=a+b+ab
b⋅a=b+a+ab
From (1) and (2), we get
axb=b⋅a
Hence,{}⋅ is commutative.
Associative: For any a,b,c∈R−{−1}
To prove:a⋅(b⋅c)=(a⋅b)⋅c
a⋅(b⋅c)=a⋅(b+c+bc)
=a+(b+c+bc)+a(b+c+bc)
=a+b+c+ab+ac+bc+abc
(a⋅b)⋅c=(a+b+ab)⋅c
=a+b+ab+c+(a+b+ab)c
=a+b+c+ab+bc+ca+abc
From (3) and (4), we have
a⋅(b⋅c)=(a⋅b)⋅c
Hence,a⋅b is associative.
Identity element:
Lete be the identity element. Then,
axe=exa=a
axe=a+e+ae=a
e(1+a)=0
Therefore, e=0[because a≠q−1]
Hence, the identity element for is e=0.
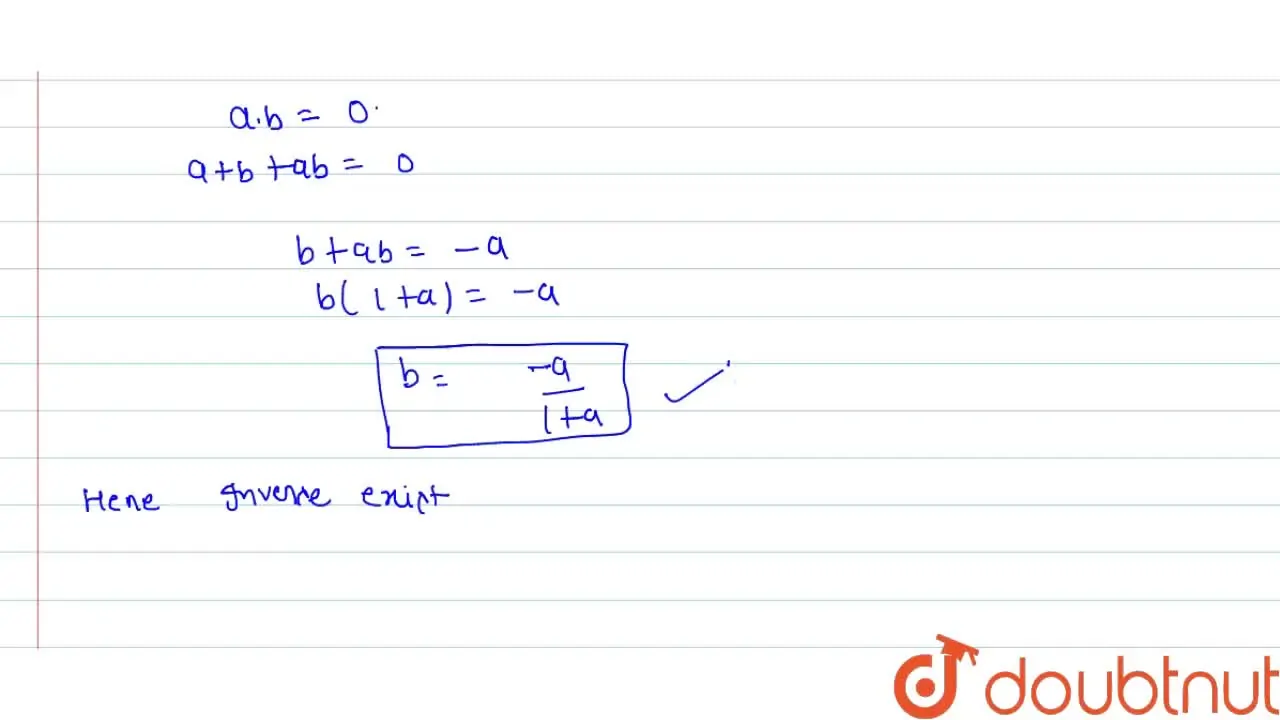
Existence of inverse: Let a=R−{−1}and b be the inverse of a.
Then,a⋅b=e=b⋅a
⇒a⋅b=e⇒a+b+ab=0⇒b=−aa+1
Since,
a∈R−(−1)
therefore a≠q−1
⇒a+1≠q0
⇒b=−aa+1∈R
Also,−aa+1=−1⇒−a=−a−1⇒−1=0, which is not possible.
Hence,−aa+1∈R−(−1)
So, every element of R−{−1}is invertible and the inverse of an element a is−aa+1.
Related Playlists
Similar Questions
Let * be a binary operation on Q−{−1} defined by a*b=a+b+ab for all a, b∈Q−{−1} . Then, Show that * is both commutative and associative on Q−{−1} . (ii) Find the identity element in Q−{−1}
View SolutionOn the set Z of integers a binary operation * is defined by a⋅b=ab+1 for all a, b∈Z . Prove that * is not associative on Z.
View SolutionOn R−[1] , a binary operation * is defined by a⋅b=a+b−ab . Prove that * is commutative and associative. Find the identity element for * on R−[1]. Also, prove that every element of r−[1] is invertible.
View SolutionShow that the binary operation * on A=R−{−1} defined as a⋅b=a+b+ab for all a,bA is commutative and associative on A. Also find the identity element of ⋅ in A and prove that every element of A is invertible.
View SolutionOn Z , the set of all integers, a binary operation * is defined by a⋅b=a+3b−4 . Prove that * is neither commutative nor associative on Z.
View SolutionLet 'o' be a binary operation on the set Q0 of all non-zero rational numbers defined by a o b=ab2 , for all a, b∈Q0 . Show that 'o' is both commutative and associate (ii) Find the identity element in Q0 (iii) Find the invertible elements of Q0 .
View SolutionA binary operation ∗ on Z defined by a∗b=3a+b for all a, b∈Z , is (a) commutative (b) associative (c) not commutative (d) commutative and associative
View SolutionLet '∗' be a binary operation defined on N×N by :
(a,b)∗(c,d)=(a+c,b+d).
Prove that '∗' is commutative and associative.View SolutionLet * be a binary operation o Q defined by a*b= ab4 for all a,b∈ Q ,find identity element in Q
View SolutionLet A be a set having more than one element. Let * be a binary operation on A defined by a⋅b=a for all a, b∈A. Is * commutative or associative on A ?
View Solution