abcd(1)sqrp
abcd(2)rsqp
abcd(3)qspr
abcd(4)qrsp
The correct Answer is:C
a. cos2A+cos2B+cos2C=−1
⇒−1−4cosAcosBcosC=−1
⇒cosAcosBcosC=0
⇒cosA=0orcosB=0orcosC=0
Thus, triangle is right angled.
b. tanA>0,tanB≥0andtanAtanB<1
tanC=tanA+tanBtanAtanB−1<0
∴∠C>90∘.
c. cos3A+cos3B+cos3C=3cosAcosBcosC
⇒(cosA+cosB+cosC)(cos2A+cos2B+cos2C−cosAcosB−cosBcosC−cosAcosC)=0
⇒cotA+cosB+cosC=0
or cos2A+cos2B+cos2C−coAcosB−cosBcosC−cosAcosC=0
⇒1+4sin(A/2)sin(B/2)sin(C/2)=0
or cosA=cosB=cosC
⇒sin(A/2)sin(B/2)sin(C/2)=−1/4( which is not possible as sin(A/2),sin(B/2),sin(C/2)>0)
orcosA=cosB=cosC
Thus, triangle is equilateral.
d. cotA>0,cotB>0andcotAcotB<1
∴tanA>0,tanB>0andtanAtanB>1
∴tanC>0
∴∠C<90∘
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)2videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type6videos
TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS
Similar Questions
Match List I with List II and select the correct answer using the codes given below the lists :
 01:37View Solution
01:37View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
06:07View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
02:11View SolutionIf sec x + tan x =22/7 , find the value of tanx/2
01:31View SolutionHow many lines of symmetry does the above figure have ?
02:45View SolutionWhich of the following are correct chain isomers of butane ? (i)
02:17View SolutionDetermine the point of symmetry of a regular hexagon.
05:41View SolutionDtermine the images of the following figure about the given line :
02:21View SolutionMatch the following Column A to Column B
 02:03View Solution
02:03View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionFind the area of the figure given below.
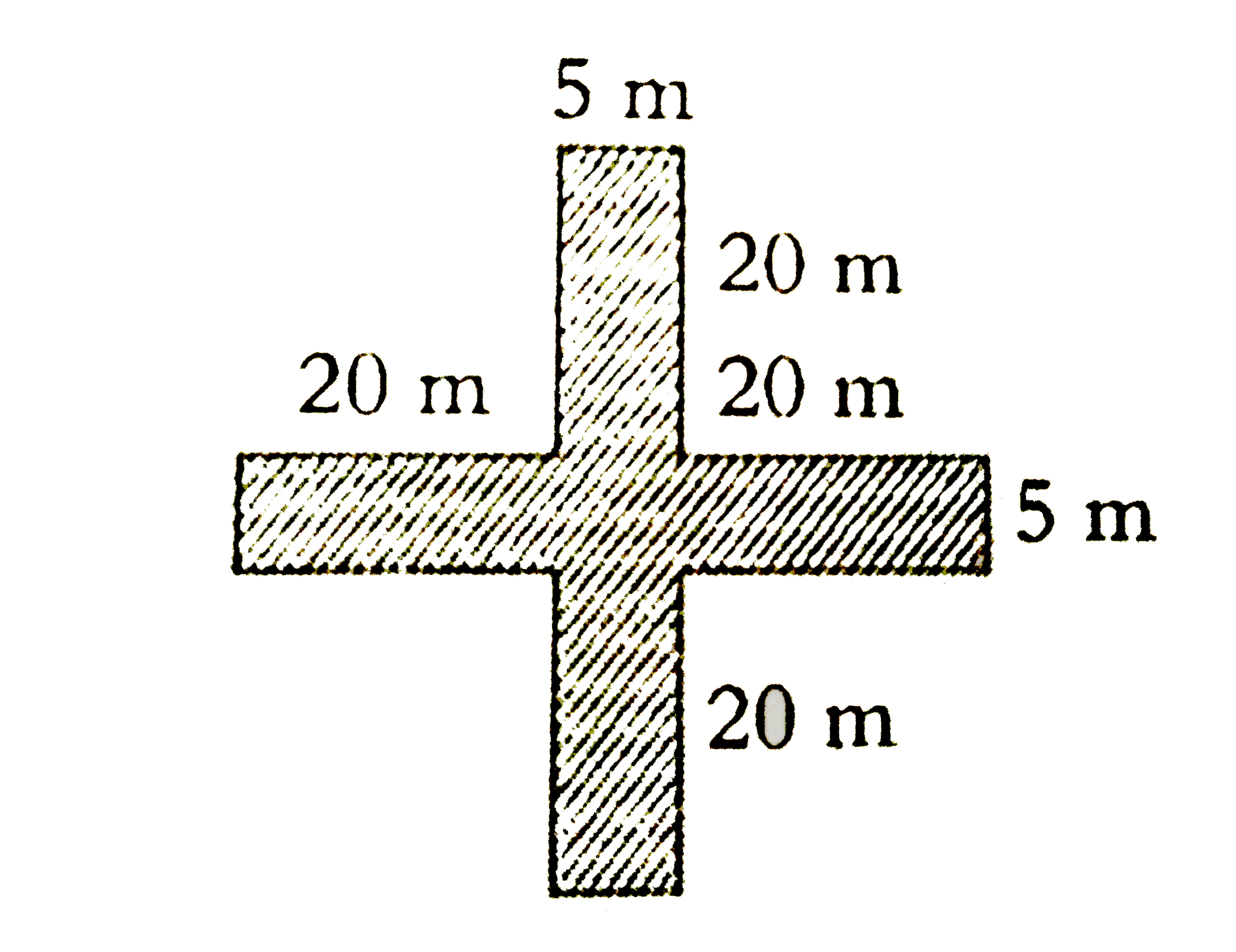 02:10View Solution
02:10View SolutionThe area of the shaded part in the figure given below is ______.
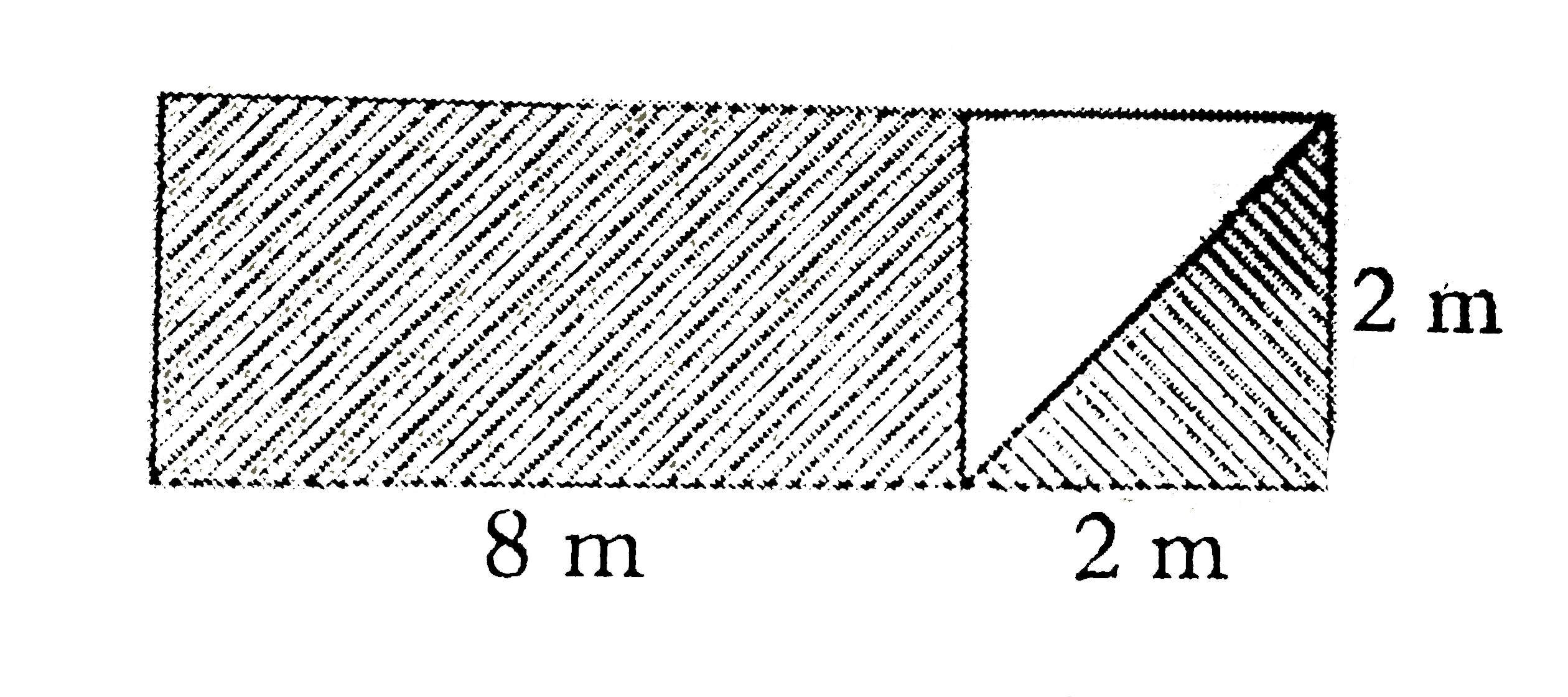 04:23View Solution
04:23View SolutionThe inequation represented by the graph given below is :
01:13View SolutionThe inequation that best describes the graph given below is _________
03:12View SolutionThe inequation that best describes the following graph is _________
05:46View Solution



