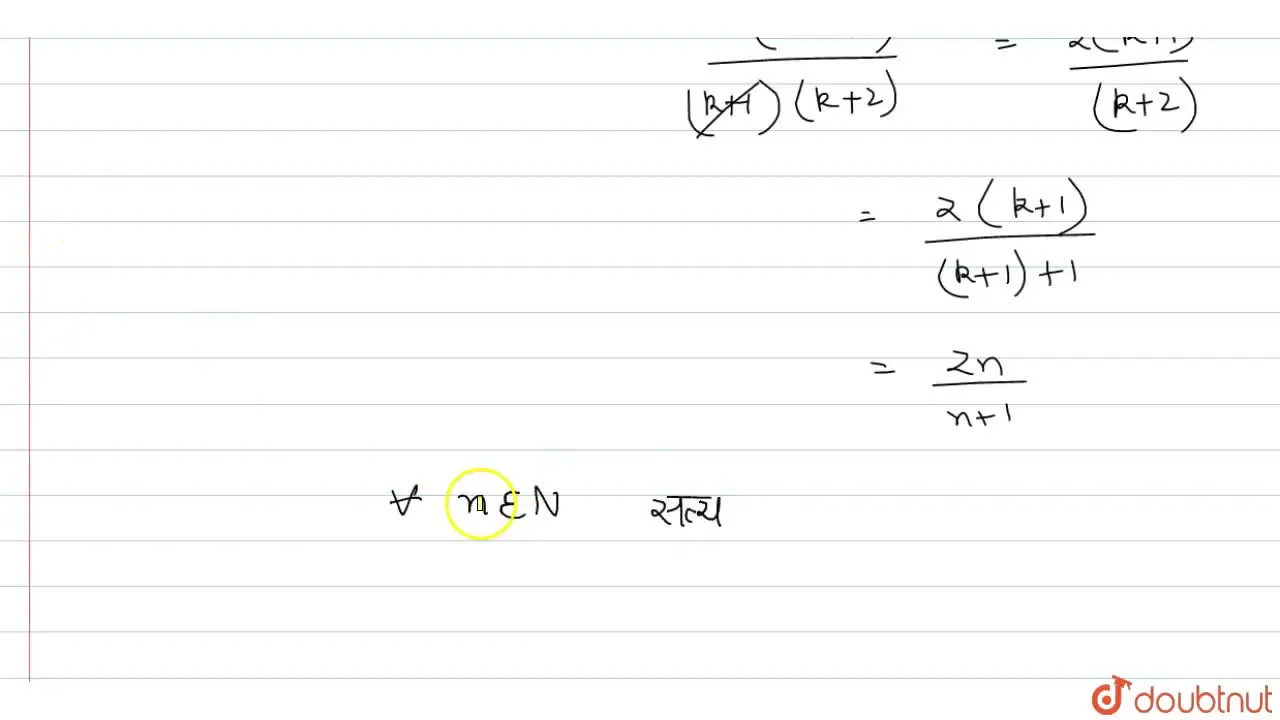n≠N के लिए गणितीय आगमन के सिद्धान्त से सिद्ध कीजिए -
1+11+2+11+2+3+...+11+2+3+...+n=2nn+1
The correct Answer is:=2(m+1)×(m+1)2m+2=2(m+1)m+2=2(m+1)(m+1+1)
अत: दिया हुआ कथन n = m + 1 के लिए भी सत्य है | अत: गणितीय आगमन के सिद्धान्त से दिया हुआ कथन n के सभी धन पूर्णाक मानो के लिए सत्य है |
Step by step video, text & image solution for n ne N के लिए गणितीय आगमन के सिद्धान्त से सिद्ध कीजिए - 1 + (1)/(1 + 2) + (1)/(1 + 2 + 3) + ...+ (1)/(1 + 2 + 3 + ...+ n) = (2n)/(n+1) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
यदि secx=135 हो और x चतुर्थ चतुर्थांश में स्थित है तो अन्य पांच त्रिकोणमितीय फलनों के मान ज्ञात कीजिए ।
03:47View Solution((2n+1)!)/((2n-1)!)*((n-1)!)/((n+2)!)=(3)/(5)
02:58View Solution1+(1)/(1+2)+(1)/(1+2+3)+(1)/(1+2+3+n)=(2n)/(n+1)
05:03View SolutionProve that 11×22×33××nn≤[(2n+1)/3]n(n+1)/2,n∈N.
05:44View SolutionIf n is a positive integer, prove that 1−2n+2n(2n−1)2!−2n(2n−1)(2n−2)3!++(−1)n−12n(2n−1)(n+2)(n−1)!=(−1)n+1(2n)!/2(n!)2.
05:12View SolutionThe sum of the series 12+32+52+....... n terms is a.n(n+1)(2n+1)2 b. n(2n−1)(2n+1)3 c. (n−1)2(2n+1)6 d. (2n+1)33
08:18View Solution1+1(1+2)+1(1+2+3)+...+1(1+2+3+...n)=2n(n+1).
05:17View SolutionIf 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!=(n+1)!−1 then show that, 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!+(n+1)(n+1)!=(n+2)!−1
09:05View Solution(1+3/1)(1+5/4)(1+7/9)...(1+((2n+1))/n^(2))=(n+1)^(2) forall n in N.
04:20View Solutionसिद्ध कीजिए की :
1n+1+12(n+1)2+13(n+1)3+..........=1n−12n2+13n3−..........03:23View Solution(2nn2+1)+13(2nn2+1)3+15(2nn2+1)5+....=
07:20View Solution1+1(1+2)+1(1+2+3)+.....+1(1+2+3+...n)=2n(n+1)
04:26View SolutionIf 1n+1+12(n+1)2+13(n+1)3+….=
λ(1n−12n2+13n3−……) then λ=05:42View SolutionIf n is a positive integer, prove that 1−2n+2n(2n−1)2!−2n(2n−1)(2n−2)3!++(−1)n−12n(2n−1)(n+2)(n−1)!=(−1)n+1(2n)!/2(n!)2.
03:00View SolutionIf n is a positive integer, prove that 1−2n+2n(2n−1)2!−2n(2n−1)(2n−2)3!++(−1)n−12n(2n−1)(n+2)(n−1)!=(−1)n+1(2n)!/2(n!)2.
06:04View SolutionProve that 11⋅22⋅33....nn≤(2n+13)n(n+1)2.
07:18View Solution