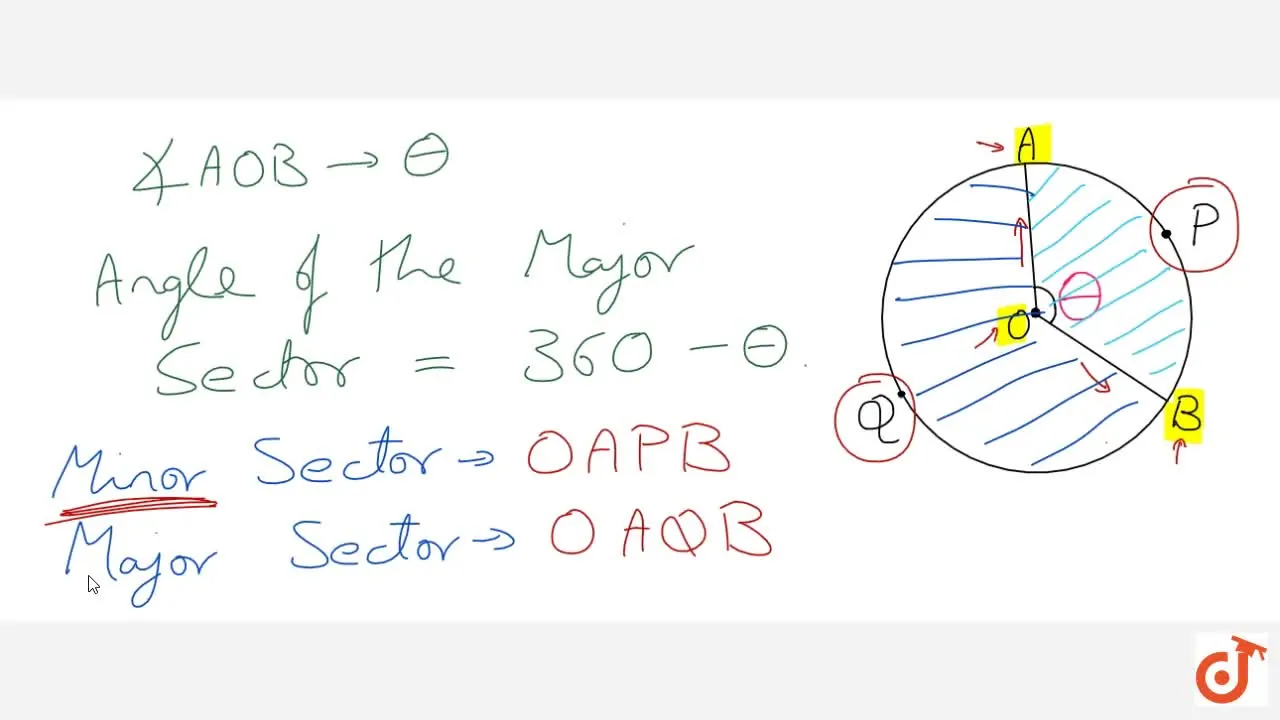
Minor and major sector
Step by step video & image solution for Minor and major sector by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
If central angle of an arc is 60∘ then the ratio of areas of minor sector and major sector will be
View SolutionMinor and major arcs
View SolutionDiscussion OF exercise-12.1 || area OF ring || Major and minor segment || Area OF major and minor sector || Area OF major and minor segment || Arc || Arc length OF major and minor segment
View SolutionA chord of a circle of radius 15 cm subtends an angle of 60∘ at the centre . Find the areas of the corresponding minor and major segments of the circle.
View SolutionIn the given figure, name the following:
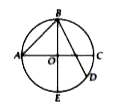
two minor and major arcsView SolutionIntroduction||Defination OF locus||Locus OF circle,Locus OF perpendicular Bisector||Equation OF Circle in cartesian format ||Semicircle,Minor and Major arc||Segment and Sector
View SolutionIf the area of a circle is 200 cm2 and that of the minor sector is 50cm2 , then the area of the corresponding major sector is
View SolutionRadius of a circle is 10cm. Area of a sector is 100cm∘. Find the area of its corresponding major sector, (π=3.14).
Given Radius of a circle =10cm
Area of sector =A=100cm2,π=3.14
To Find: Area of corresponding major sector
Formula: (i) Are of a circle =πr2
A(major sector) =A(circle)-A(minor sector)View SolutionFind the difference of the area of a sector of angle 90∘ and its coresponding major sector of a circle of radius 9.8 cm
View SolutionFind the area of the sector of a circle with 4cm and of angle 30∘. Also find the area of the corresponding major sector.
View Solution