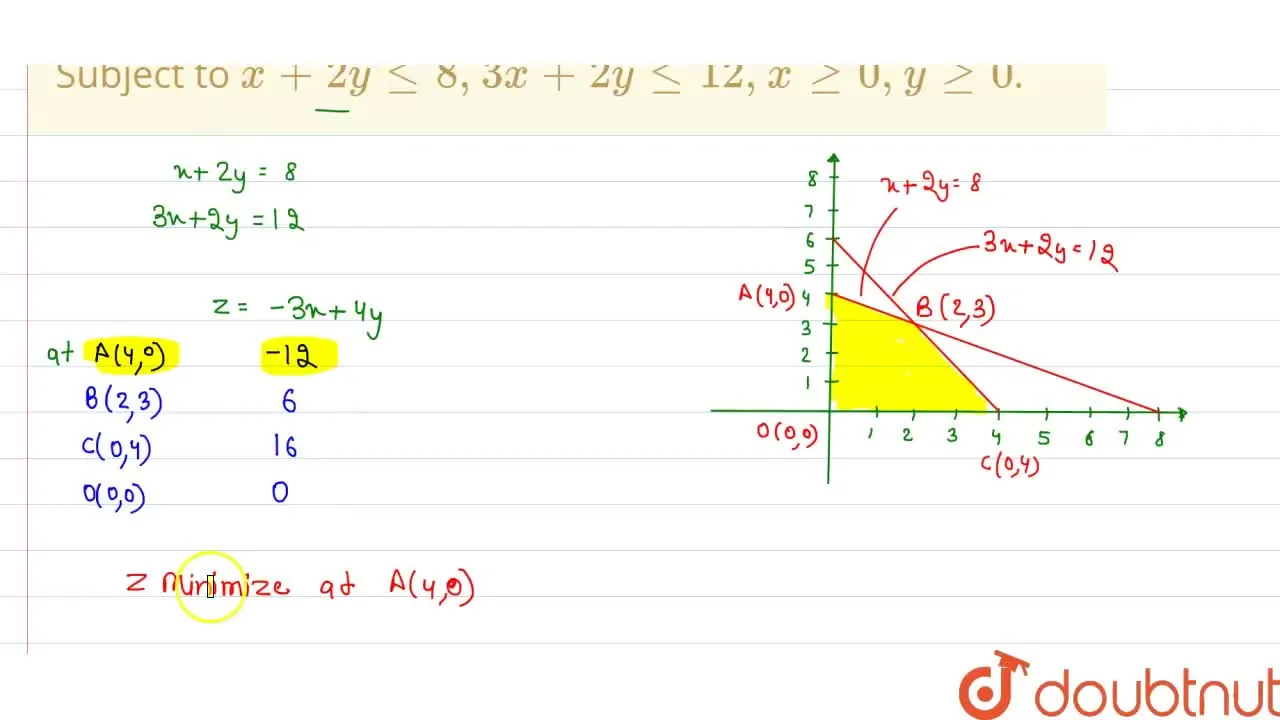
Minimise Z=−3x+4y
Subject to x+2y≤8,3x+2y≤12,x≥0,y≥0.
Minimise Z−3x+4y………………..1
Subject to
x+2y≤8…………………….2
3x+2y≤12…………………..3
x≥0,y≥0…………….4
First we draw the graph of the line x+2y=8
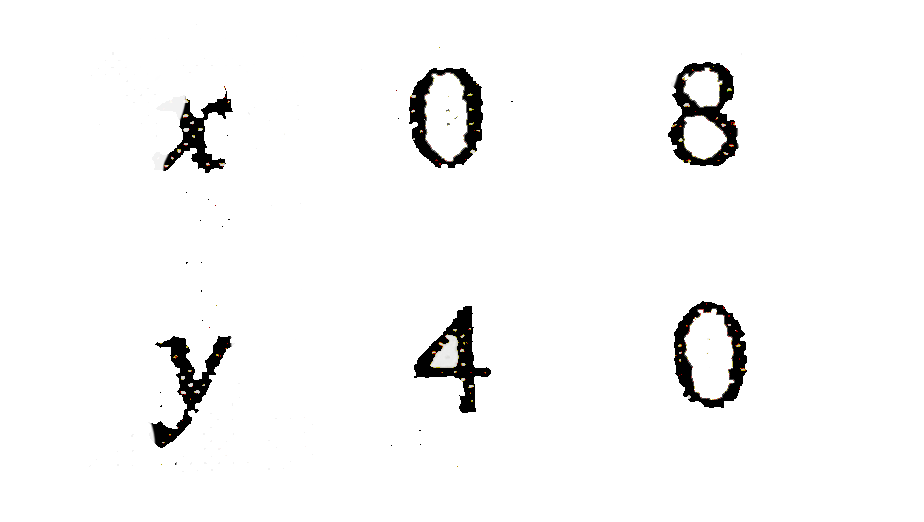
Put (0,0) in the inequation x+2y≤8,
0+0≤8⇒0≤8 (True)
 ltBrgt Therefore half plane contains the origin.
ltBrgt Therefore half plane contains the origin.
Since x,y≥0
Therefore feasible region is in first quadrant.
Now, draw the graph of the line 3x+2y=12
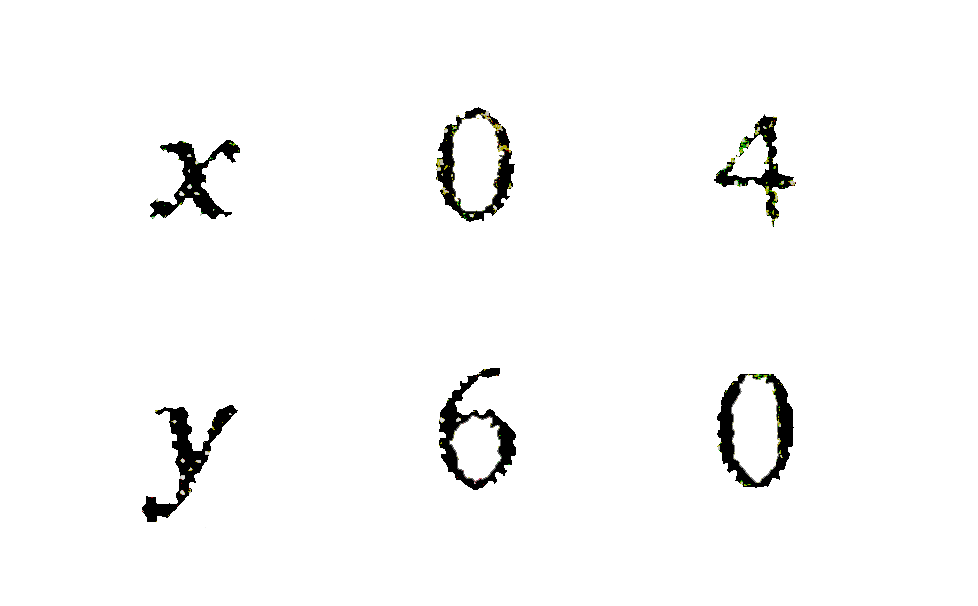
Put (0,0) in the inequation 3x+2y≤12
3×0+2×0≤12⇒0≤12 (True)
∴Feasible region is OABCO.
From the equations x+2y=8 and 3x+2y=12, we get x=2 and y=3.
∴ Point of intersection is B(2,3).
Thus, the vertices of the feasible region are O(0,0),A(4,0),B(2,3) and C(0,4). We find the value of Z at these points.
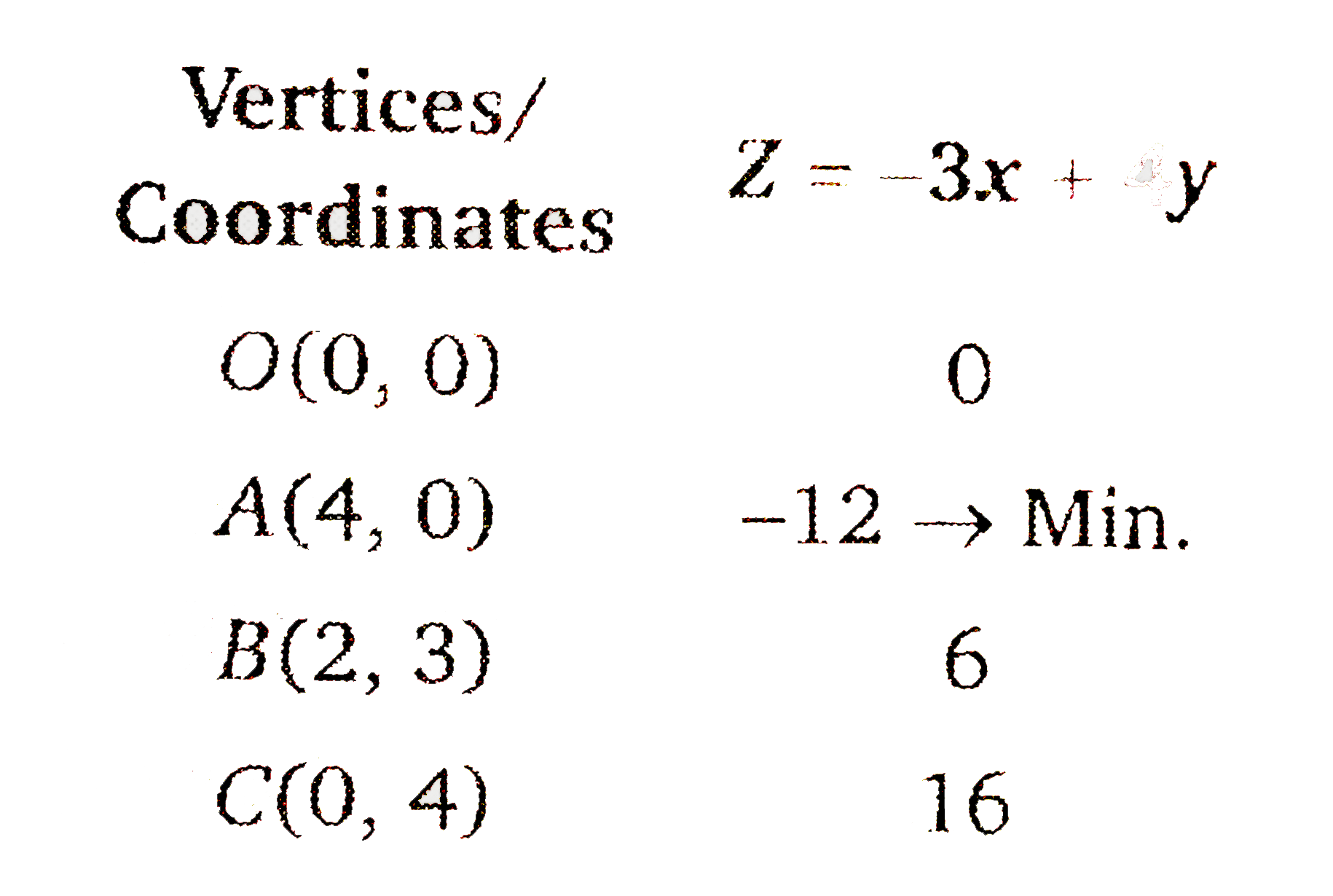
Therefore, minimum value of Z is −12 which is at the point A(4,0).
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.211videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise9videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 B15videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )9videos
INVERES TRIGONOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice15videos
MATRICES
Similar Questions
Maximise Z=5x+3y
Subject to 3x+5y≤15,5x+2y≤10,x≥0,y≥0.View SolutionMaximise Z=3x+2y
Subject to x+2y≤10,3x+y≤15,x,y≥0View SolutionSolve the following linear programming problem graphically:
Maximize : z=30x+25y
Subject to: x+y≤6
3x+2y≤15
x≥0
y≥0View SolutionSolve the following linear programming problem graphically:
Minimize: z=x+3y
Subject to:
x+y≤8
3x+5y≥15
x≥0
y≥0View SolutionMaximise Z=x+y
Subject to x−y≤−1,−x+y≤0,x,y≥0.View SolutionMinimise and Maximise Z=5x+10y
Subject to x+2y≤120,x+y≥60,x−2y≥0,y≥0.View SolutionMaximise Z=3x+4y
Subject to the constraints
x+y≤4,x≥0,y≥0View SolutionSolve the following linear programming problem graphically:
Minimize : z=200x+500y
Subject to: x+2y≥10
3x+4y≤24
x≥0
y≥0View SolutionMinimise and Maximise Z=x+2y
Subject to x+2y≥100,2x−y≤0,2x+y≤200,x,y≥0.View SolutionSolve the Following Linear Programming Problem graphically : Minimise Z=x+2ysubject to 3x+y≥3,x+2y≥6.x,y≥0.
View Solution