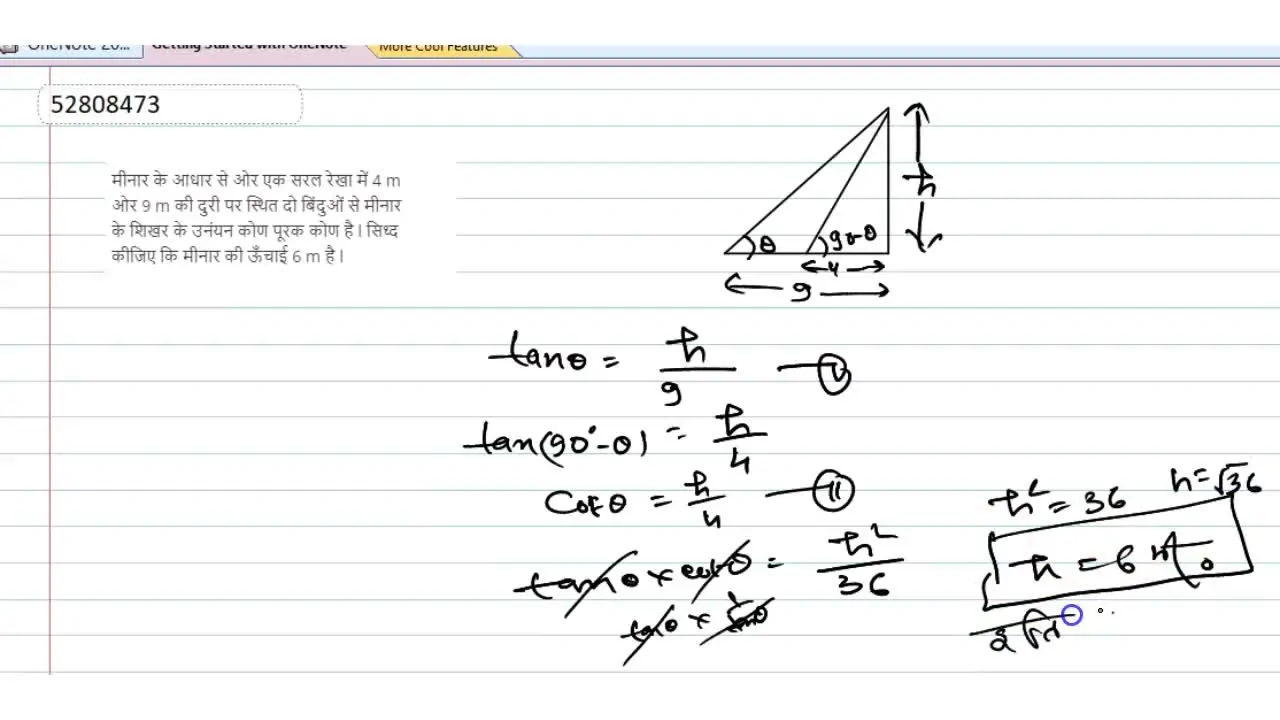
मीनार के आधार से ओर एक सरल रेखा में 4 m ओर 9 m की दुरी पर स्थित दो बिंदुओं से मीनार के शिखर के उनंयन कोण पूरक कोण है l सिध्द कीजिए कि मीनार की ऊँचाई 6 m है l
Step by step video & image solution for मीनार के आधार से ओर एक सरल रेखा में 4 m ओर 9 m की दुरी पर स्थित दो बिंदुओं से मीनार के शिखर के उनंयन कोण पूरक कोण है l सिध्द कीजिए कि मीनार की ऊँचाई 6 m है l by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोगEXERCISE - प्रश्नावली 9(B)8videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोगEXERCISE - लघु उत्तरीय2videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोगEXERCISE - लघु उत्तरीय2videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति का परिचय EXERCISE - प्रश्नावली 8(E)17videos
त्रिकोणमिति का परिचय
- BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6(F)17videos
त्रिभुज
Similar Questions
एक ऊर्ध्वाधर खम्भे कि परछाईं, खम्भे कि ऊँचाई के बराबर है । सूर्य का उन्नयन कोण होगा :
01:21:49View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर : खड़ा हैं । टॉवर के ठीक सामने दूसरे के एक अन्य बिंदु से टॉवर शिखर का उन्नयन कोण 60∘ है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30∘ है (देखिए आकृति) । टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए ।
 01:24:42View Solution
01:24:42View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर : खड़ा हैं । टॉवर के ठीक सामने दूसरे के एक अन्य बिंदु से टॉवर शिखर का उन्नयन कोण 60∘ है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30∘ है (देखिए आकृति) । टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए ।
 03:00View Solution
03:00View Solutionप्रतेक प्रश्न के चार उत्तर दिये है। सही उत्तर छाँटकर लिखिए।
यदि sinθ=35 तो tanθ का मान है:02:14View Solutionसमद्विबाहु त्रिभुज की तीनों भुजाओं के मध्य बिन्दुओं को मिलाने से बना त्रिभुज होता है :
03:59View Solutionदो समतलीय का सह-तलीय होना|दो समतलों के बीच कोण#!#समतल से दिए गए बिंदु की दूरी#!#एक रेखा एवं एक समतल के बीच कोण#!#उदाहरण
04:38View Solutionदो रेखाओ के मध्य कोण |बिन्दु से रेखा पर लंब
03:32View Solutionएक रेखा की दिक्-कोसाइन ज्ञात कीजिए तो निर्देशांक्षो के साथ समान कोण बनाती है |
01:38View SolutionA tower stands on the top of a building which is 40 metres high. The angle of depressiotf of a point situated on the ground-from the top and bottom of the tower are found to Be 60∘ and 45∘ respectively.What is the height (in metres) of tower?
एक भवन जिसकी ऊँचाई 40 मीटर है, के शिखर पर एक मीनार खड़ी है। मीनार के शिखर तथा पांद बिन्दु से भूमि पर स्थित एक बिन्दु का अर्वनमन कोण क्रमशः 60∘ तथा 45∘ है। मीनार की ऊँचाई (मीटर में) क्या है ?46:01View SolutionFrom a point P, the angle of elevation of a tower is such that its tangent is 3/4. On walking 560 meters towards the tower the tangent of the angle of the elevation of the tower becomes 4/3. What is the height (in meters) of the tower?
एक बिंदु P से, एक टावर की ऊँचाई का कोण ऐसा है कि इसकी स्पर्शरेखा 3/4 है। टॉवर को ओर 560 मीटर चलने पर टॉवर के ऊंचाई के कोण के स्पर्शरेखा 4/3 हो जाती है। मीनार की ऊँचाई (मीटर में) कितनी है?46:43View SolutionThe height of a tower is, 300 meters. When its top is seen from top of another tower, then the angle of depression is 60∘. The horizontal distance between the bases of the two towers is 120 metres. What is the height (in meters) of the small tower?
एक मीनार की ऊँचाई 300 मीटर है। जब उसकी चोटी की दूसरे मीनार की चोटी से देखा जाता है, तो उन्नयन कोण 60∘ का होता है। दोनों मीनारें के आधारों के मध्य को दूरी 120 मीटर हैं छोटे मीनार की ऊँचाई (मीटर में) क्या है?51:40View SolutionHeight of a tower is 120 metres. The angle of elevation of the top of tower from a point B is 75^@ .Point B is on the ground level. What is the distance (in metres)of point B from the base of tower? एक भीनार की ऊँचाई 120 मीटर है। बिंदु B से मीनार की चोटी का उन्नयन कोण 75^@ है। बिंदु B जमीन की सतह पर है। मीनार के आधार से बिंदु B की दूरी (मीटर में) क्या है?
03:43View SolutionThe angle of elevation of a tower from a distance 50m from its foot is 30^@ . The height of the tower is- एक मीनार का उसके मूल आधार (पाद) से 50 मीटर दूरी से उन्नयन कोण 30^@ है। तदनुसार उस मीनार की ऊँचाई कितनी होगी?
03:25View Solutionसमांतर रेखाएं ओर तिर्यक रेखा |कोण की स्थिति के आधार पर वर्गीकरण |तिर्यक रेखा से बनने वाले कोणो से संबंधित अभिगृतियाँ |प्रमेय|एक ही रेखा के समांतर रेखाएं |प्रमेय|अभ्यास कार्य |सारांश
04:30View Solutionसमांतर रेखाएं ओर तिर्यक रेखा |कोण की स्थिति के आधार पर वर्गीकरण |तिर्यक रेखा से बनने वाले कोणो से संबंधित अभिगृतियाँ |प्रमेय|अभ्यास कार्य |सारांश
02:27View Solutionसमांतर रेखाएं ओर तिर्यक रेखा |कोण की स्थिति के आधार पर वर्गीकरण |तिर्यक रेखा से बनने वाले कोणो से संबंधित अभिगृतियाँ |प्रमेय|NCERT प्रश्नावली |सारांश
01:39View Solution