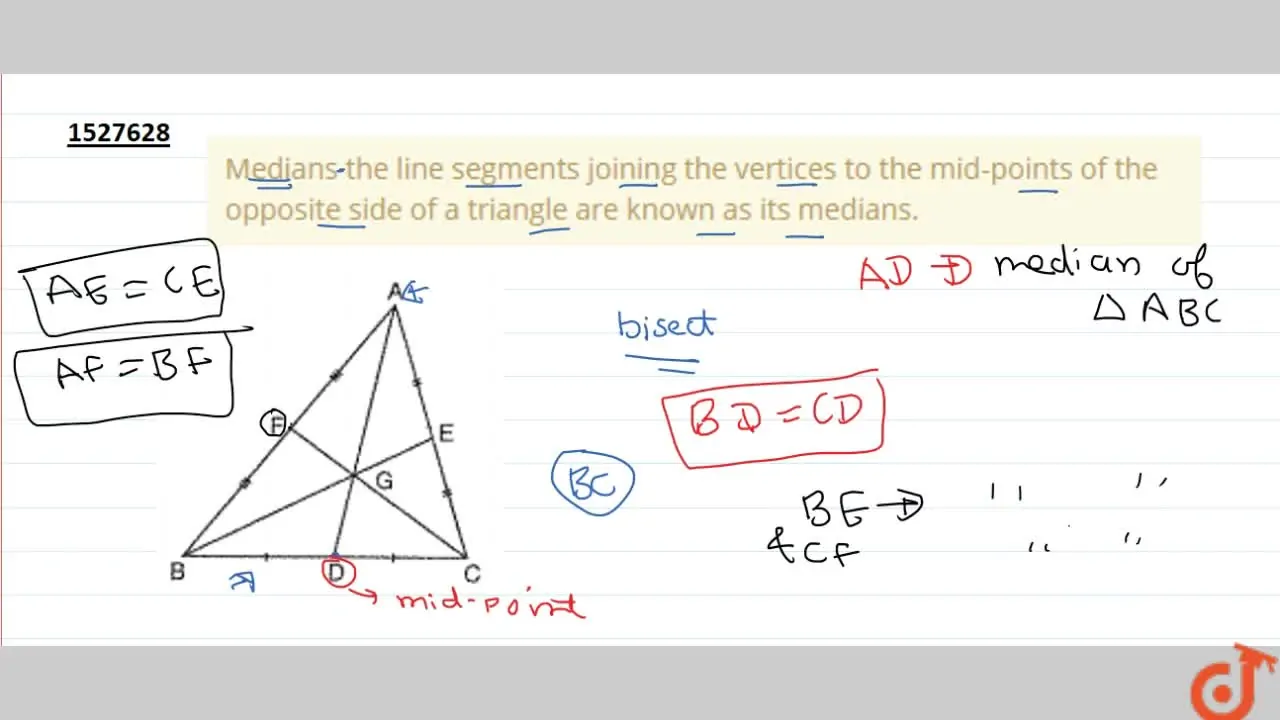
Medians the line segments joining the vertices to the mid-points of the opposite side of a triangle are known as its medians.
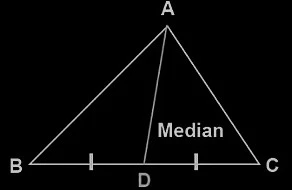
Median
You are familiar with the term ‘triangle’ and its properties. Before we try to explore more about them, we need to get some good information on some of their basic properties. We know that a three-sided polygon which has 3 vertices and 3 sides enclosing 3 angles is called a triangle.
A triangle can be classified into scalene, isosceles and equilateral based on the length of its sides. On the basis of interior angles, a triangle can be an obtuse-angled, acute-angled, or right-angled triangle. We also need to know that the sum of interior angles in a triangle is 180 degrees.
So, in this chapter, we will learn how to draw medians of a triangle. We will also concentrate on the properties of medians of a triangle as well to get the perfect idea about it.
What is the Median of a Triangle?
When a line segment joins a vertex to the mid-point of the side and that too it is opposite to that vertex, it is known as a median of the triangle. Look at the below figure where the median AD divides BC into two equal halves, i.e., DB = DC.
Properties of Median of a Triangle
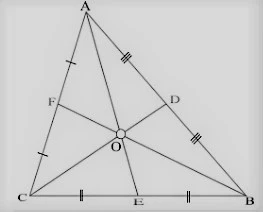
Coming to the properties of median of a triangle, they are as follows:
- There are 3 medians in every triangle, one from each vertex. The 3 medians of the triangle ABC are AE, BF and CD.
- It is always in a single point that the 3 medians irrespective of the shape of the triangle is.
- The triangle is cut into two smaller triangles by each median of a triangle which have equal areas.
- The point where the 3 medians meet is known as the centroid of the triangle. The centroid of the triangle ABC is point O.
- The triangle is divided into 6 smaller triangles of equal area by the 3 medians.
How to Find the Median of a Triangle?
If a, b and c are considered to be the lengths of the sides and m is the median from interior angle A to side a, then we can find the median of a triangle as:
m = √ 2b2 + √ 2c2 – a2/4
Related Videos:
- Interior
- Exterior
- Triangular Region
- Sides of triangle, Angles of triangle, Six part of elements of the triangle
Altitude of Triangle
The line segment that starts from the vertex and meets the opposite side at right angles is termed as an altitude of a triangle.
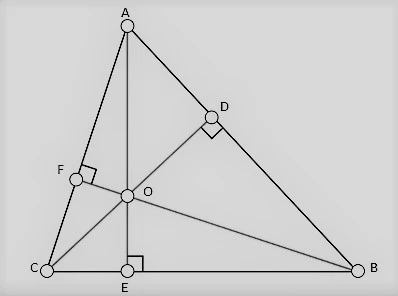
Properties of Altitudes of a Triangle
Let us have a look at the different properties of altitudes of a triangle:
- There are 3 altitudes in every triangle, one from each vertex. The 3 altitudes of the triangle ABC are AE, BF and CD.
- It is at a single point that the 3 altitudes always meet, no matter what the shape of the triangle is.
- The altitude happens to be the shortest distance from the vertex to its opposite side.
- The ortho-centre of the triangle is the point where the 3 altitudes meet. Point O happens to be the ortho-centre of the triangle ABC.
- When it comes to the altitude of a triangle, it may lie inside or outside the triangle.
Important Chapters:



Similar Questions
Line segments joining the vertices to the mid-points of the opposite sides to a triangle are known as medians (b) altitudes (c) heights (d) angle bisectors
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionThe line segment joining a vertex of a triangle to the mid-point of its opposite side is called its __________.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionProve that the sum of the vectors directed from the vertices to the mid-points of opposite sides of a triangle is zero.
View SolutionIf the coordinates of the mid-points of the sides of a triangle are (3,4),(4,6)and(5,7), find its vertices.
View SolutionLine joining the mid-point of a side of a triangle to opposite vertex is Median
View SolutionProve that the line segment joining the mid points of two sides of a triangle is parallel to its third side.
View SolutionThe line segment joining the mid-points of any two sides of a triangle is parallel to the third side of a triangle.
View Solution