Match the statements of column A and Column B.

Text Solution
(i) Given that, z=−i+√−3=r(cosθ+sinθ)
∵rcosθ=√3,rsinθ=1
⇒r2==1+3=4⇒r=2[∵r>0]
⇒tanα=∣∣∣rsinθrconsθ∣∣∣=1√3
⇒tanα=1√3⇒α=π6
∵x>0,y>0
and arg (z)=θ=π6
So tha polor form of z is 2(cosπ6+isin(π)6).
(ii) Given that, z−1+√−3=−1+i√3
∴tanα=∣∣∣√3−1∣∣∣=√3
⇒tanθα=tanπ3⇒α=π3

∵x<0,y>0
θ=π−α=π=π3=2π3
(iii) Given that, |z+2|=|z−2|
⇒|x+2+iy|=|x−2+iy|
⇒(x+2)2+y2=(x−2)2y2
⇒x2+4x+4=x2−4x+4⇒8x=0
∴x=0
"It is a traight line which is a perpendicular biscector of segment joining the point" (−2,0)and(2,0).
(iv) Given that, |z+2i|=|z−2i| ltbtgt ⇒|x+i(y+2)|=|x+i(y−2)|
⇒x2+(y=2)2=x2+(y−2)2
⇒4y=0⇒y=0
"It is a straight line, which is a perpendicular bisector of segment joining" (0,−2)and(0,2)
(v) Given that, |z+4i|≥3=|x+iy+4i|≥3
⇒=|x+i(y+4)|≥3
⇒=√x2+(y+4)2≥3
⇒x2+(y+4)2≥9
⇒=x2+y2+8y+16≥9
=x2+y2+8y+7≥0
which represent a circle. On or outside having centre (0. -4) and radius 3.
(vi) Given that, |z+3|≤3
⇒|x+iy+4|≤3
⇒|x+4+iy|≤3
rA√(x+4)2+y2≤3
⇒(x+4)2+y2≤9
⇒x2+8x+16+y2≤9
⇒x2+8x+y2+7≤0
It represent the region which is on or inside the circle having the centre (-4, 0) and radius 3 .
(vii) Given that," " z=1+2i1−i=(1+2i)(1+i)(1−i)(1+i)
= (1+2i+i2i)21−i2=1−2−3i1+1=−1+3i2
∴ ¯z=−12−3i2
Hence, (−12,−32) "lies in third quadrant".
(viii) Given that, z = 1-i
Hence, " " (12,12)
"Hence, the correct matches are(a)→(v),(b)→(iii),(c)→(i),(d)→(iv),(e)→(ii),(f)→(vi),(g)→(viii),(h)→(vii)
|
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:NCERT EXEMPLAR ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:OBJECTIVE TYPE QUESTIONS
Explore 16 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:NCERT EXEMPLAR ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:LONG ANSWER TYPE QUESTIONS
Explore 14 Videos
- BINOMIAL THEOREMBook:NCERT EXEMPLAR ENGLISHChapter:BINOMIAL THEOREMExercise:True/False
Explore 7 Videos
- CONIC SECTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONIC SECTIONSExercise:Objective type
Explore 13 Videos
Similar Questions
Knowledge Check
Match the statements of Column A and with those of Column B
 AA→c,B→b,C→d,D→aBA→c,B→d,C→b,D→aCA→c,B→d,C→a,D→bDA→d,B→c,C→a,D→b
AA→c,B→b,C→d,D→aBA→c,B→d,C→b,D→aCA→c,B→d,C→a,D→bDA→d,B→c,C→a,D→bMatch the statements of Column A and with those of Column B

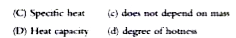 ADACBBACBDCACDBDBCDA
ADACBBACBDCACDBDBCDAMatch the statements of Columne A with values of Columne B
 A(i)−(A),(ii)−(B),(iii)−(C),(iv)−(D)B(i)−(C),(ii)−(D),(iii)−(A),(iv)−(B)C(i)−(B),(ii)−(D),(iii)−(C),(iv)−(A)D(i)−(A),(ii)−(D),(iii)−(C),(iv)−(B)
A(i)−(A),(ii)−(B),(iii)−(C),(iv)−(D)B(i)−(C),(ii)−(D),(iii)−(A),(iv)−(B)C(i)−(B),(ii)−(D),(iii)−(C),(iv)−(A)D(i)−(A),(ii)−(D),(iii)−(C),(iv)−(B)
Match the statements in column A with those in column B

View SolutionMatch the statements in column A, with those in column B

View SolutionMatch the statements in column A with those in column B,

View SolutionMatch the statements in column A with those in column B.

View SolutionMatch the statements of Column A with those of Column B.

View Solution



