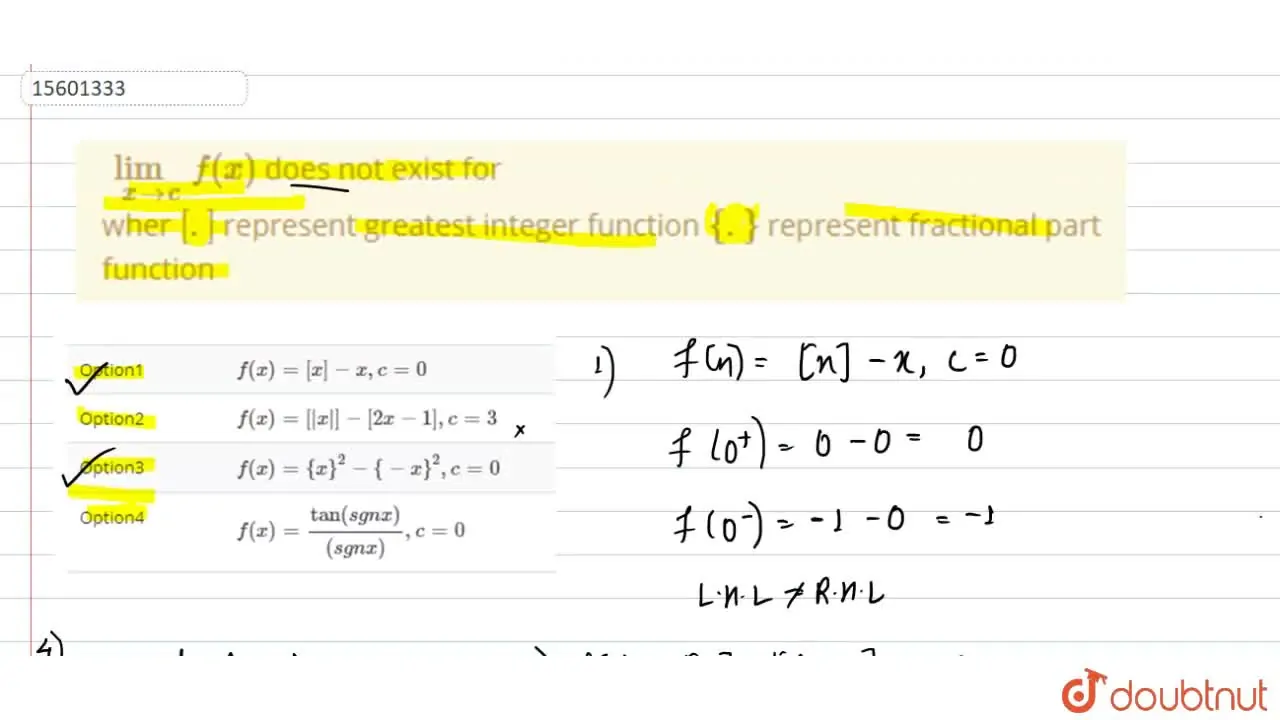
limx→cf(x) does not exist for
wher [.] represent greatest integer function {.} represent fractional part function
f(x)=[x]−x,c=0
f(x)=[|x|]−[2x−1],c=3
f(x)={x}2−{−x}2,c=0
f(x)=tan(sgnx)(sgnx),c=0
The correct Answer is:A, C, D
(A) limx→3[|x|]−[2x−1]
R.H.L x=3−⇒f(3+)=3−5=−2
L.H.L x=3−⇒f3−=2−4=−2
(B) f(0+)=0−0=0,f(0−)=−1
(C) f(x)=(x−[x])2−(−x−[−x])2
f(0+)=0−(+1)2=−1
f(0−)=(0−1)−(0−0)2=1
(D) f(0+)=tan11=tan1
f(0−)=tan(−1)−1=tan1
Related Playlists
Similar Questions
[.] represents greatest integer function:
 View Solution
View SolutionProve that limx→2[x] does not exists, where [.] represents the greatest integer function.
View Solution[2x]−2[x]=λ where [.] represents greatest integer function and {.} represents fractional part of a real number then
View Solutionlimx→0[100tanxsinxx2] is (where [.] represents greatest integer function).
View SolutionFInd limx→α+[min(sinx,{x})x−1] where alpha is the root of the equation sinx+1=x Here [.] represents greatest integer function and {.} represents fractional part function
View SolutionGreatest Integer Function ( Inequation ) || Fractional Part Function
View Solutionlimx→cf(x) does not exist when
where [.] and {.} denotes greatest integer and fractional part of xView SolutionThe set of all values of x satisfying {x}=x[×] where [×] represents greatest integer function {×} represents fractional part of x
View SolutionEvaluate: (lim)x→0sinxx,where[.] represents the greatest integer function.
View SolutionThe value of limx→πsgn[tanx], where [.] represents greatest integer function,
View Solution