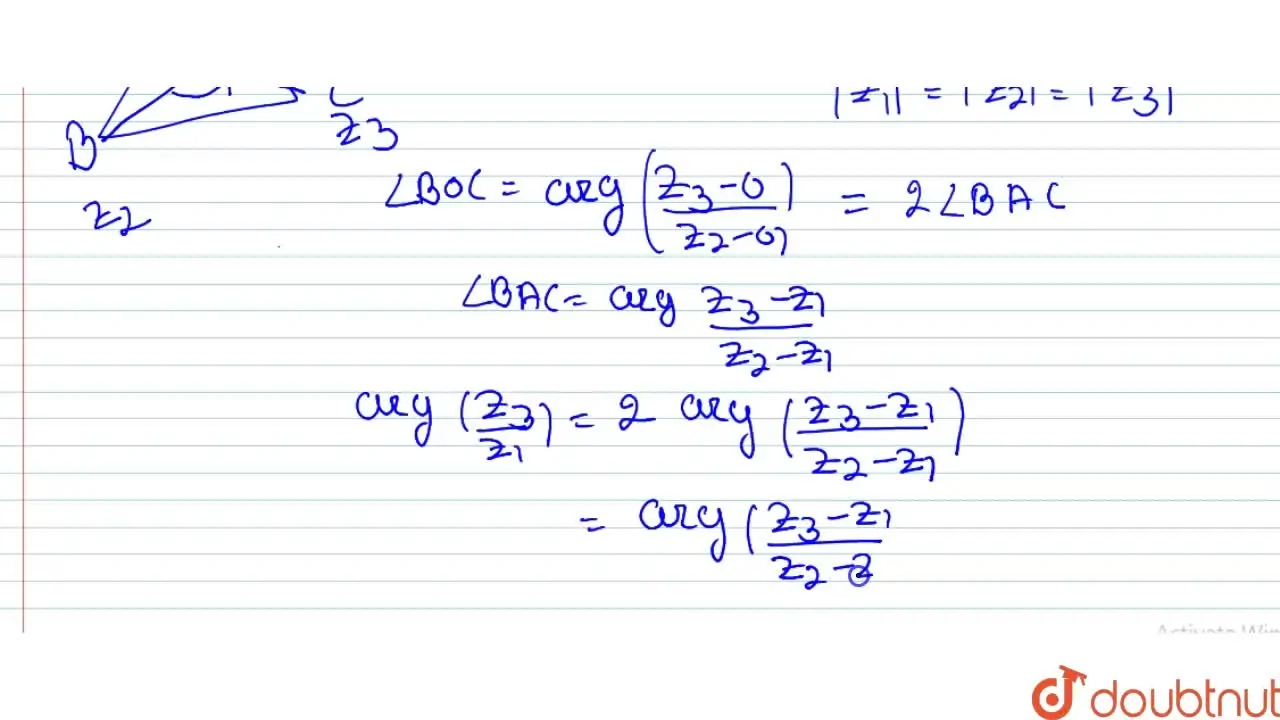Let z1,z2,z3 be the three nonzero complex numbers such that z2≠1,a=|z1|,b=|z2|andc=|z3|. Let |abcbcacab|=0 arg(z3)z2=arg(z3−z1z2−z1)2 orthocentre of triangle formed by z1,z2,z3,isz1+z2+z3 if triangle formed by z1,z2,z3 is equilateral, then its area is 3√32|z1|2 if triangle formed by z1,z2,z3 is equilateral, then z1+z2+z3=0
Step by step video & image solution for Let z_1, z_2, z_3 be the three nonzero complex numbers such that z_2!=1,a=|z_1|,b=|z_2|a n d c=|z_3|dot Let |a b c b c a c a b|=0 a r g(z_3)/(z_2)=a r g((z_3-z_1)/(z_2-z_1))^2 orthocentre of triangle formed by z_1, z_2, z_3, i sz_1+z_2+z_3 if triangle formed by z_1, z_2, z_3 is equilateral, then its area is (3sqrt(3))/2|z_1|^2 if triangle formed by z_1, z_2, z_3 is equilateral, then z_1+z_2+z_3=0 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
If z1,z2,z3 are complex numbers such that |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1 then |z1+z2+z3| is equal to
View SolutionIf z1,z2,z3 are complex numbers such that |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1 then |z1+z2+z3| is equal to
View SolutionIf z1,z2,z3 are three complex numbers such that |z1|=|z2|=1, find the maximum value of |z1−z2|2+|z2−z3|2+|z3+z1|2
View SolutionIf z1,z2,z3 are distinct nonzero complex numbers and a,b,c∈R+ such that a|z1−z2|=b|z2−z3|=c|z3−z1| Then find the value of a2z1−z2+b2z2−z3+c2z3−z1
View SolutionIf z1,z2,z3 are three complex numbers such that 5z1−13z2+8z3=0, then prove that ⎡⎢ ⎢⎣z1(¯z)11z2(¯z)21z3(¯z)31⎤⎥ ⎥⎦=0
View SolutionIf |z1−1|<1, |z2−2|<2,|z3−3|<3 then |z1+z2+z3|
View SolutionLet z1,z2andz3 be three complex numbers such that z1+z2+z3=z1z2+z2z3+z1z3=z1z2z3=1. Then the area of triangle formed by points A(z1),B(z2)andC(z3) in complex plane is _______.
View SolutionLet z1,z2 and z3 be three distinct complex numbers , satisfying |z1|=|z2|=|z3|=1 find maximum value of| z1 - z2 |^2 + |z2-z3|^2 + |z3-z1|^2
View SolutionIf |z|=2andz1−z3z2−z3=z−2z+2 , then prove that z1,z2,z3 are vertices of a right angled triangle.
View SolutionIf 2z1−3z2+z3=0, then z1,z2andz3 are represented by
View Solution