Let →AB=3ˆi+ˆj−ˆkand→AC=ˆi−ˆj+3ˆk and a point P on the line segment BC is equidistant from AB and AC, then −−→AP is
2ˆi−ˆk
ˆi−2ˆk
2ˆi+ˆk
none of these
The correct Answer is:C
Clearly, a point equidistant from AB and AC is on the bisector of the ∠BAC.
A vector along the bisector of ∠BAC is
−−→AB∣∣∣−−→AB∣∣∣=−−→AC∣∣∣−−→AC∣∣∣=1√11(4ˆi+2ˆk)=2√11(2ˆi+ˆk)
Let −−→AP=λ(2ˆi+ˆk)
∴−−→BP=−−→AP−−−→AB=λ(2ˆi+ˆk)−(3ˆi+ˆj−ˆk)
⇒−−→BP=(2λ−3)ˆi−ˆj+(λ+1)ˆk
Also, −−→BC=−−→AC−−−→AB=−2ˆi−2ˆj+4ˆk
Since −−→BP∣∣−−→BC. Therefore,
−−→BP=t−−→BC
⇒(2λ−3)ˆi−ˆj+(λ+1)ˆk=t(−2ˆi−2ˆj+4ˆk)
⇒2λ−3=−2t,−1=−2t,λ+1=4t
⇒λ=1,t=12
∴−−→AP=2ˆi+ˆk.
Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Exercise30videos
ALGEBRA OF VECTORS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Chapter Test30videos
ALGEBRA OF VECTORS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise39videos
ALGEBRAIC INEQUATIONS
Similar Questions
In a ΔABC, if −−→AB=ˆi−7ˆj+ˆkand−−→BC=3ˆj+ˆj+2ˆk, then ∣∣∣−−→CA∣∣∣=
View SolutionIf →a=ˆi+3ˆj,→b=2ˆi−ˆj−ˆkand→c=mˆi+7ˆj+3ˆk are coplanar then find the value of m.
View SolutionIf vector →a=ˆi+ˆj+ˆk,→b=4ˆi+3ˆj+4ˆk and →c=ˆi+αˆj+βˆk are linearly dependent and |→c|=√3 , then value of |α|+|β| is
View SolutionIf a=3ˆi−2ˆj+ˆk,b=2ˆi−4ˆj−3ˆkandc=−ˆi+2ˆj+2ˆk, then a+b+c is
View SolutionLet →a=ˆi−ˆj+ˆk,→b=2ˆi+ˆj+ˆkand→c=ˆi+ˆj−2ˆk, then the value of [→a→b→c] is equal to
View SolutionLet −−→OA=ˆi+3ˆj−2ˆkand−−→OB=3ˆi+ˆj−2ˆk. Then vector −−→OC biecting the angle AOBandC being a point on the line AB is
View SolutionIf the point of intersection of the line
→r=(ˆi+2ˆj+3ˆk)+λ(2ˆi+ˆj+2ˆk) and the plane →r(2ˆi−6ˆj+3ˆk)+5=0 lies on the plane →r(ˆi+75ˆj+60ˆk)−α=0, then 19α+17 is equal to :View SolutionIf →r.(2ˆi+3ˆj−2ˆk)+32=0 is the equation of a plane and ˆi−2ˆj+3ˆk is a point then a point equidistasnt from the plane on the opposite side is
(A) ˆi+2ˆj+3ˆk (B) 3ˆi+ˆj+ˆk (C) 3ˆi+2ˆj+3ˆk (D) 3(ˆi+ˆj+ˆk)View SolutionGiven: →p=−ˆi−3ˆj+2ˆk and →r=ˆi+3ˆj+5ˆk. Find vector parallel to electric field at position r. [ Note that →p.→r=0]
View SolutionIf in the shown figure AC=ˆi+2ˆj+4ˆk and BD=ˆi−3ˆj+ˆk then BC is
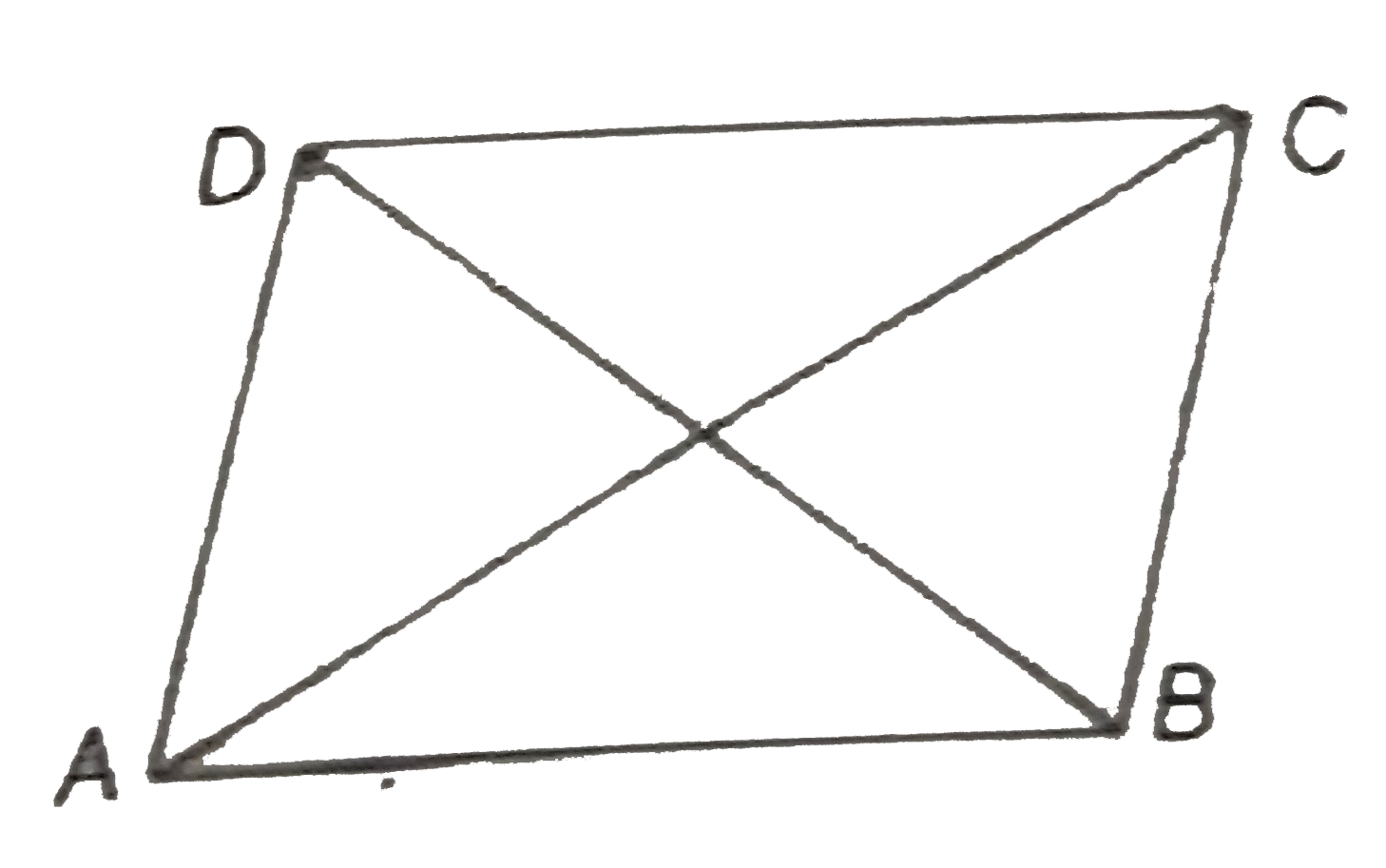 View Solution
View Solution


