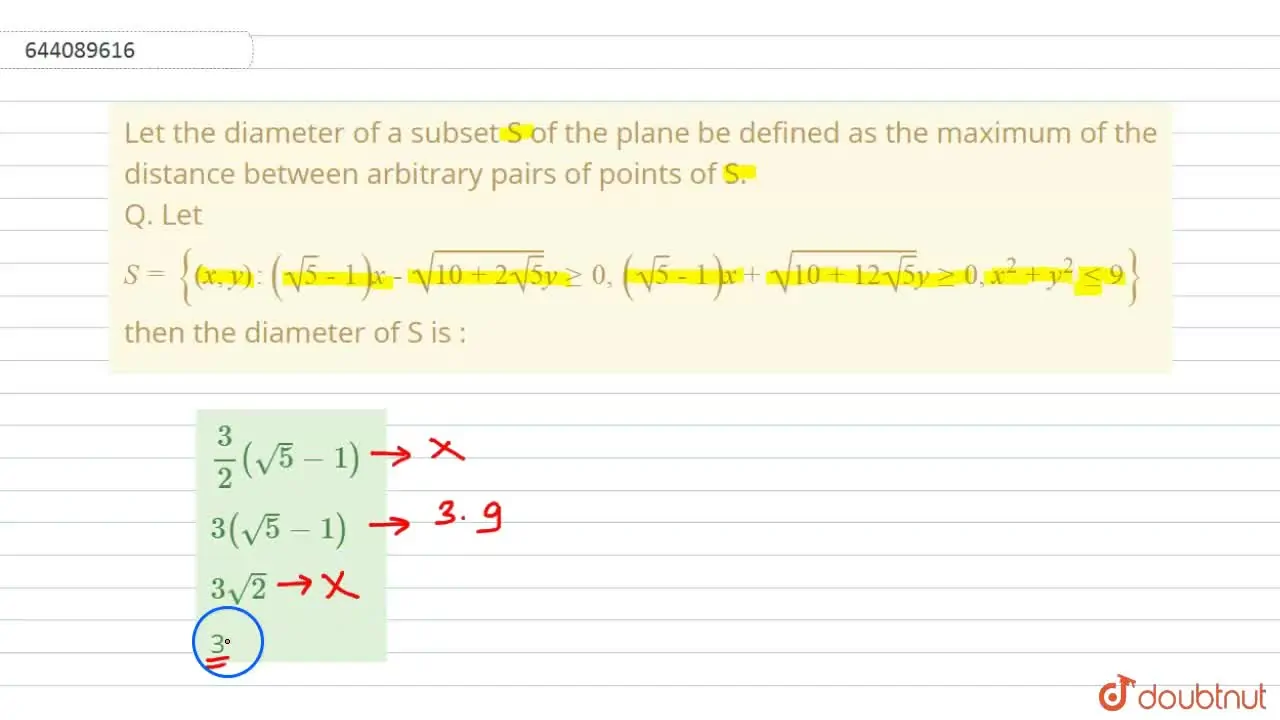
Let the diameter of a subset S of the plane be defined as the maximum of the distance between arbitrary pairs of points of S.
Q. Let S={(x,y):(√5−1)x−√10+2√5y≥0,(√5−1)x+√10+12√5y≥0,x2+y2≤9} then the diameter of S is :
32(√5−1)
3(√5−1)
3√2
3
The correct Answer is:D
Step by step video & image solution for Let the diameter of a subset S of the plane be defined as the maximum of the distance between arbitrary pairs of points of S. Q. Let S={(x,y):(sqrt(5)-1)x-sqrt(10+2sqrt(5))y ge 0, (sqrt(5)-1)x+sqrt(10+12sqrt(5)) y ge 0, x^(2)+y^(2) le 9} then the diameter of S is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VK JAISWAL ENGLISHCHAPTER - CIRCLEEXERCISE - Exercise - 5 : Subjective Type Problems12videos
CIRCLE
- BOOK - VK JAISWAL ENGLISHCHAPTER - CIRCLEEXERCISE - Exercise - 2 : One or More than One Answer is/are Correct10videos
CIRCLE
- BOOK - VK JAISWAL ENGLISHCHAPTER - BIONMIAL THEOREMEXERCISE - Exercise-4 : Subjective Type Problems16videos
BIONMIAL THEOREM
- BOOK - VK JAISWAL ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE-5 : SUBJECTIVE TYPE PROBLEMS8videos
COMPLEX NUMBERS
Similar Questions
Let the diameter of a subset S of the plane be defined as the maximum of the distance between arbitrary pairs of points of S.
Q. Let S={(x,y):(y−x)≤0,x+y≥0,x2+y2≤2} then the diameter of S is :View Solution√5x−√7y=0√7x−√3y=0
View SolutionIf 2+√52−√5 =x and 2−√52+√5 =y , find the value of x2−y2.
View SolutionIf x =√5−2√5+2 and y=√5+2√5−2 : find :
x2+y2+xyView SolutionIf x =√5−2√5+2 and y=√5+2√5−2 : find :
x2View SolutionIf x =√5−2√5+2 and y=√5+2√5−2 : find :
xyView SolutionIf x =√5−2√5+2 and y=√5+2√5−2 : find :
y2View SolutionIf x=√5−√3√5+√3andy=√5+√3√5−√3 find the value of x2+y2
View SolutionSolve √5−1sinx+√10+2√5cosx=8,x∈(0,π2)
View SolutionSolve √5−1sinx+√10+2√5cosx=8,x∈(0,π2)
View Solution