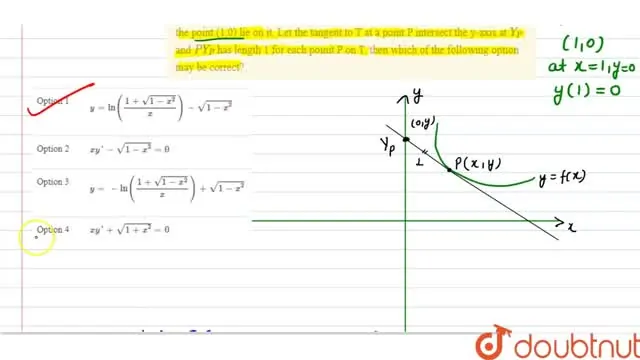
let T denote a curve which is in the first quadrant and let the point (1,0) lie on it. Let the tangent to T at a point P intersect the y-axis at and has length 1 for each poinit P on T. then which of the following option may be correct?
The correct Answer is:A, B, C, D
be differentiation of f(x) equation of tangent
put x=0
put
put x=1 and
Related Playlists
Similar Questions
Let ⌈ denote a curve y=y(x) which is in the first quadrant and let the point (1,0) lie on it . Let the tangant ot ⌈ at a point P intersect the y-axis at YP. If PYP has length l for each point P on ⌈, then which of the following options is/ are correct ?
View SolutionThe curve y=f(x) in the first quadrant is such that the y - intercept of the tangent drawn at any point P is equal to twice the ordinate of P If y=f(x) passes through Q(2,3), then the equation of the curve is
View SolutionA curve y=memx where m>0 intersects y-axis ai a point P,
What is the slope of the curve at the point of intersection P?View SolutionIf the tangent at any point P of a curve meets the axis of x in T. Then the curve for which OP=PT,O being the origins is
View SolutionLet P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve.
View SolutionFind the equation of tangent of the curve 6y=9−3x2 at point (1,1).
View SolutionLet the acute angle bisector of the two planes x−2y−2z+1=0and2x−3y−6+1=0 be the plane P. Then which of the following points lies on P ?
View SolutionLet the acute angle bisector of the two planes x−2y−2z+1=0and2x−3y−6z+1=0 be the plane P. Then which of the following points lies on P ?
View SolutionA line is tangent to the curve f(x)=413x3 at the point Pin the first quadrant, and has a slope 2009. This line intersects the y-axis at (0,b). Find the value of b
View SolutionLet P be a point in the first quadrant lying on the ellipse x28+y218=1. Let AB be the tangent at P to the ellipse meeting the x -axis at A and y axis at B. If O is the origin, then the minimum, possible area of ΔOAB is (in square units)
View Solution