Let S={xε(−π,π):x≠0,+π2}The sum of all distinct solutions of the equation √3secx+cosecx+2(tanx−cotx)=0 in the set S is equal to Solution in Tamil
−7π9
−2π9
0
5π9
The correct Answer is:C
√3secx+cosecx=2(cotx−tanx)
⇒√3cosx+1sinx=2(cosxsinx−sinxcosx)
⇒√3sinx+cosx=2(cos2x−sin2x)
⇒cos(x−π3)=cos2x
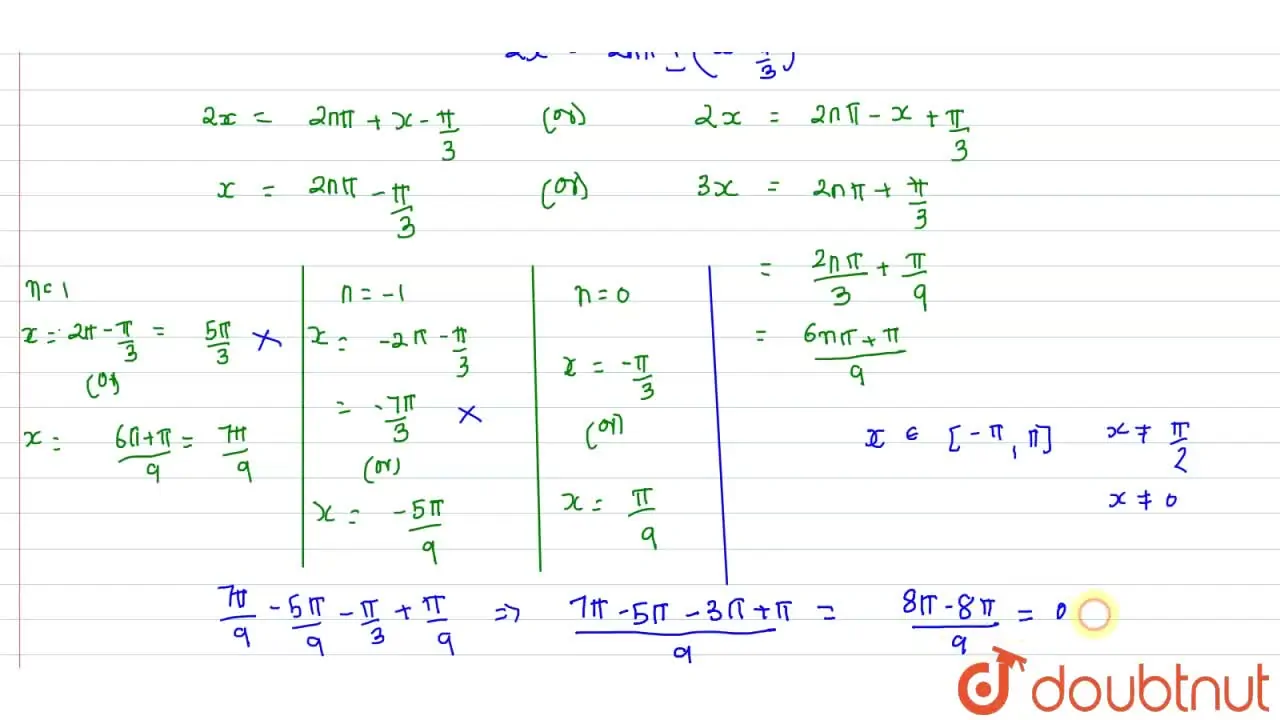
⇒2x=2nπ±(x−π3),n∈Z
⇒x=2nπ−π3,2nπ3+π9
In (−π,π),x=−π3,π9,7π9,−5π9
∴Σxi=0
Related Playlists
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - JEE Main Previous Year2videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank4videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the derivative of y=tan−12x3
04:58View SolutionIf 0≤x≤2π, then the number of real values of x, which satisfy the equation cosx+cos2x+cos3x+cos4x=0, is
06:24View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]04:36View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
05:31View SolutionThe sum of all the solution in [0,4π] of the equation tanx+cotx+1=cos(x+π4)is (a) 3π (b) π2 (c) 7π2 (d) 4π
09:16View SolutionLet S={x varepsilon(-pi,pi):x!=0,+(pi)/(2)} The sum of all distinct solutions of the equation root(3)(3)sec x+cos ecx+2(tan x-cot x)=0 in the set S is equal to
03:57View SolutionThe sum of all the solutions in [0,4π] of the equation tanx+cotx+1=cos(x+π4) is
06:44View SolutionThe solution set of inequality (cot−1x)(tan−1x)+(2−π2)cot−1x−3tan−1x−3(2−π2)>0, is
13:03View Solutionमाना कि S={x∈(−π,π),x≠0,±π2} है। समुच्चय S में समीकरण √3secx+cosec x+2(tanx−cotx)=0 के सभी भिन्न हलों (all distinct solutions) का योग (sum) है :
05:33View SolutionIf xepsilon[0, pi] the equation sinx+(1)/(2)cosx=sin^(2)(x+(pi)/(4)) Defines, then the sum of all such values of x is
02:51View SolutionLet S={x∈(−π,π):x≠0,±π2}. The sum of all distinct solutions of the equation √3secx+cosecx+2(tanx−cotx)=0 in the set S is equal to
09:16View SolutionLet S={t∈R:f(x)=|x−π|(e|x|−1)sin|x| is not differentiable at t} Then the set S is equal to: (1) ϕ (2) {0} (3) {π} (4) {0,π}
03:01View SolutionLet S={x∈(−π,π),x≠0±π2}. The sum of all distinct solution is of the equation √3secx+(cosecx+2(tanx−cotx)=0 in the set S=
03:20View SolutionIf the equation tan(Pcotx)=cot(Ptanx) has a solution in x∈(0,π)−{π2} , then
06:44View Solutionमाना कि S={x∈(−π,π),x≠0,±π2} है। समुच्चय S में समीकरण √3secx+cosec x+2(tanx−cotx)=0 के सभी भिन्न हलों (all distinct solutions) का योग (sum) है : (i) −7π9 (ii) −2π9 (iii) 0 (iv) 5π9
View Solution