Let PQ be a double ordinate of the hyperboalx2a2−y2b2=1.If O be the centre of the hyperbola and OPQ is an equilateral triangle, then prove that the eccentricity e >2√3.Solution in Bengali
Step by step video & image solution for Let PQ be a double ordinate of the hyperboal(x^(2))/(a^(2))-(y^(2))/(b^(2)) = 1.If O be the centre of the hyperbola and OPQ is an equilateral triangle, then prove that the eccentricity e gt 2/sqrt(3). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABook:CHHAYA PUBLICATIONChapter:HYPERBOLAExercise:MULTIPLE CHOICE TYPE QUESTIONS
Explore 20 Videos
- HYPERBOLABook:CHHAYA PUBLICATIONChapter:HYPERBOLAExercise:VERY SHOT ANSWER TYPE QUESTIONS
Explore 16 Videos
- DIAGRAMMATIC REPRESENTATION OF DATABook:CHHAYA PUBLICATIONChapter:DIAGRAMMATIC REPRESENTATION OF DATAExercise:EXERCISE (Very short Answer Type Question)
Explore 7 Videos
- MATHEMATICAL INDUCTION Book:CHHAYA PUBLICATIONChapter:MATHEMATICAL INDUCTION Exercise:Sample Questions for Competitive Exams
Explore 20 Videos
Similar Questions
If e is the eccentricity of the hyperbola x2a2−y2b2=1 , then e =
View SolutionExplain what geometrical diagrams are represented by the equatio x2a2+y2a2(1−e2)=1, where a and e are constants.
View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
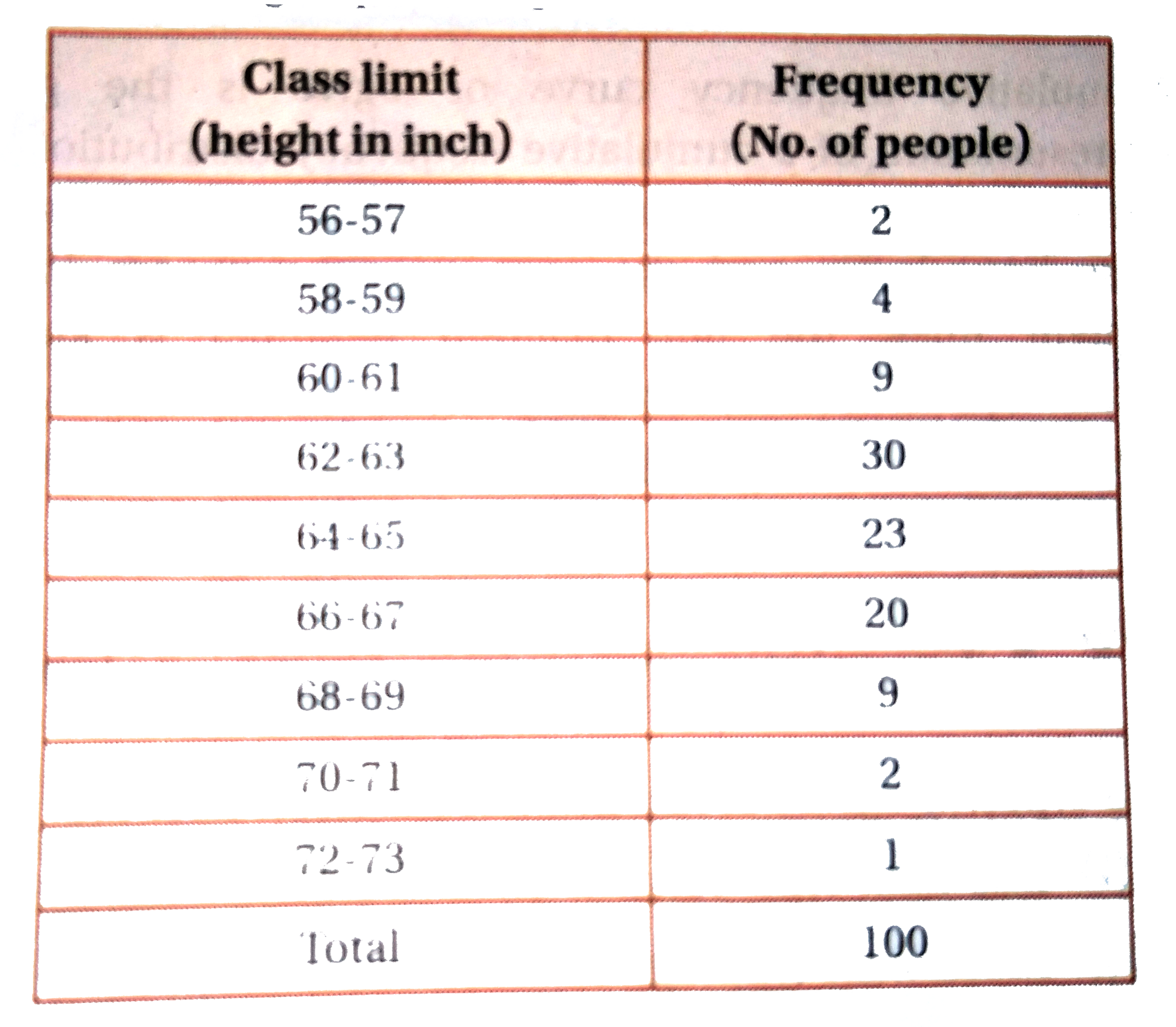 Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
View SolutionAB is double ordinate of the hyperbola (x^(2))/(a^(2))-(y^(2))/(b^(2))=1 such that Delta AOB( where 'O' is the origin) is an equilateral triangle,then the eccentricity e of hyperbola satisfies:
View SolutionIf PQ is a double ordinate of the hyperbola x2a2−y2b2=1 such that OPQ is an equilateral triangle, O being the center of the hyperbola, then find the range of the eccentricity e of the hyperbola.
View SolutionIf PQ is a double ordinate of the hyperbola x2a2−y2b2=1 such that ΔOPQ is equilateral, O being the centre. Then the eccentricity e satisfies
View SolutionPQ is double ordinate of the hyperbola x2/a2−y2/b2=1 such that OPQ is an equilateral triangle , O being the centre of hyperbola . The eccentricity of the hyperbola satisfies
View Solutionx2a2−y2b2=1 পরাবৃত্তের PQ একটি দ্বিগুণ কোটি। যদি পরাবৃত্তের কেন্দ্র O এবং OPQ একটি সমবাহু ত্রিভুজ হয়, তবে প্রমাণ করো যে, e>2√3।
View Solutiono কেন্দ্রীয় পরাবৃত্ত x2a2−y2b2=1-এর PQ একটি দ্বিগুণ কোটি। ΔOPQ একটি সমবাহু ত্রিভুজ হলে পরাবৃত্তটির উৎকেন্দ্রতা e এর জন্য নীচের কোনটি সঠিক?
View SolutionIf hyperbola x^2/a^2-y^2/b^2=1 Problem category PQ Is as follows OPQ Is an equilateral triangle where O Is the center of the hyperbola
View SolutionPQ is a double ordinate of the hyperbola x2a2−y2b2=1 such that OPQ is an equilateral triangle, O being the center of the hyperola, then prove that the eccentricity e of the hyperbola satisfies e>2√3.
View SolutionIf PQ is a double ordinate of the hyperbola such that OPQ is an equilateral triangle, being the centre of the hyperbola, then eccentricity e of the hyperbola satisfies
View SolutionIf PQ is a double ordinate of the hyperbola x2a2−y2b2=1 such that OPQ is an equilateral triangle, O being the center of the hyperbola, then find the range of the eccentricity e of the hyperbola.
View SolutionIf PQ is a double ordinate of the hyperbola x2a2−y2b2=1 such that OPQ is an equilateral triangle, O being the center of the hyperbola, then find the range of the eccentricity e of the hyperbola.
View Solution

