Let P be a point on x2=4y. The segment joining A(0,−1) and P is divided by point Q in the ratio 1:2, then locus of point Q is
9x2=3y+2
9x2=12y+8
9y2=12x+8
9y2=3x+2
The correct Answer is:B
To find the locus of point Q, which divides the segment joining point A (0, -1) and point P on the parabola x2=4y in the ratio 1:2, we can follow these steps:
Step 1: Identify the coordinates of point P
Since point P lies on the parabola x2=4y, we can express the coordinates of point P in terms of a parameter t. The parametric equations for the parabola are:
P(2t,t2)
Step 2: Use the section formula to find the coordinates of point Q
Point Q divides the segment joining A (0, -1) and P (2t, t^2) in the ratio 1:2. According to the section formula, if a point Q divides the segment joining points A (x1,y1) and B (x2,y2) in the ratio m:n, then the coordinates of point Q are given by:
Q(mx2+nx1m+n,my2+ny1m+n)
Here, m=1, n=2, A(0,−1), and P(2t,t2).
Substituting the values:
Q(1⋅2t+2⋅01+2,1⋅t2+2⋅(−1)1+2)=Q(2t3,t2−23)
Step 3: Set the coordinates of Q in terms of x and y
Let the coordinates of Q be:
Q(x,y)⇒x=2t3andy=t2−23
Step 4: Express t in terms of x
From the equation x=2t3, we can express t as:
t=3x2
Step 5: Substitute t into the equation for y
Now substitute t into the equation for y:
y=t2−23=(3x2)2−23
Calculating t2:
t2=(3x2)2=9x24
Now substituting this back into the equation for y:
y=9x24−23=9x2−812
Step 6: Rearranging the equation
Multiplying both sides by 12 to eliminate the fraction:
12y=9x2−8
Rearranging gives us the final equation:
9x2=12y+8
Final Result
Thus, the locus of point Q is given by:
9x2=12y+8
Since point P lies on the parabola x2=4y, we can express the coordinates of point P in terms of a parameter t. The parametric equations for the parabola are:
P(2t,t2)
Point Q divides the segment joining A (0, -1) and P (2t, t^2) in the ratio 1:2. According to the section formula, if a point Q divides the segment joining points A (x1,y1) and B (x2,y2) in the ratio m:n, then the coordinates of point Q are given by:
Q(mx2+nx1m+n,my2+ny1m+n)
Here, m=1, n=2, A(0,−1), and P(2t,t2).
Q(1⋅2t+2⋅01+2,1⋅t2+2⋅(−1)1+2)=Q(2t3,t2−23)
Let the coordinates of Q be:
Q(x,y)⇒x=2t3andy=t2−23
From the equation x=2t3, we can express t as:
t=3x2
Now substitute t into the equation for y:
y=t2−23=(3x2)2−23
Calculating t2:
t2=(3x2)2=9x24
Now substituting this back into the equation for y:
y=9x24−23=9x2−812
Multiplying both sides by 12 to eliminate the fraction:
12y=9x2−8
Rearranging gives us the final equation:
9x2=12y+8
Thus, the locus of point Q is given by:
9x2=12y+8
Similar Questions
Knowledge Check
- Question 1 - Select One
If P is the point (1,0) and Q is any point on the parabola y2=8x then the locus of mid - point of PQ is
AP1 lies on C2andQ1 lies on C1BPQ≥min{PP1,QQ1}Cpoint P0 on C1 such that P0Q0≤PQ for all pairs of points (P,Q) is (13,109)Dpoint Q0 on C2 such that P0Q0≤PQ for all pairs of points (P,Q) is (109,13) - Question 2 - Select One
P is a point on the line segment joining the points (3,2,−1)and(6,2,−2). If the x-coordinate of P is 5, then its y-coordinate is
A1B−1C2D−2
The line segment joining the points A(3,2) and B (5,1) is divided at the point P in the ratio 1:2 and it lies on the line 3x−18y+k=0. Find the value of k.
View SolutionLet (x,y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionLet (x,y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionLet O be the vertex and Q be any point on the parabola,x2=8y . It the point P divides the line segment OQ internally in the ratio 1 : 3, then the locus of P is : (1) x2=y (2) y2=x (3) y2=2x (4) x2=2y
View SolutionIf the point P (−1,2) divides the line segment joining A (2,5) and B in the ratio 3:4 , find the co-ordinate of B .
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
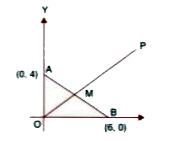
co-ordinates of PView Solution
