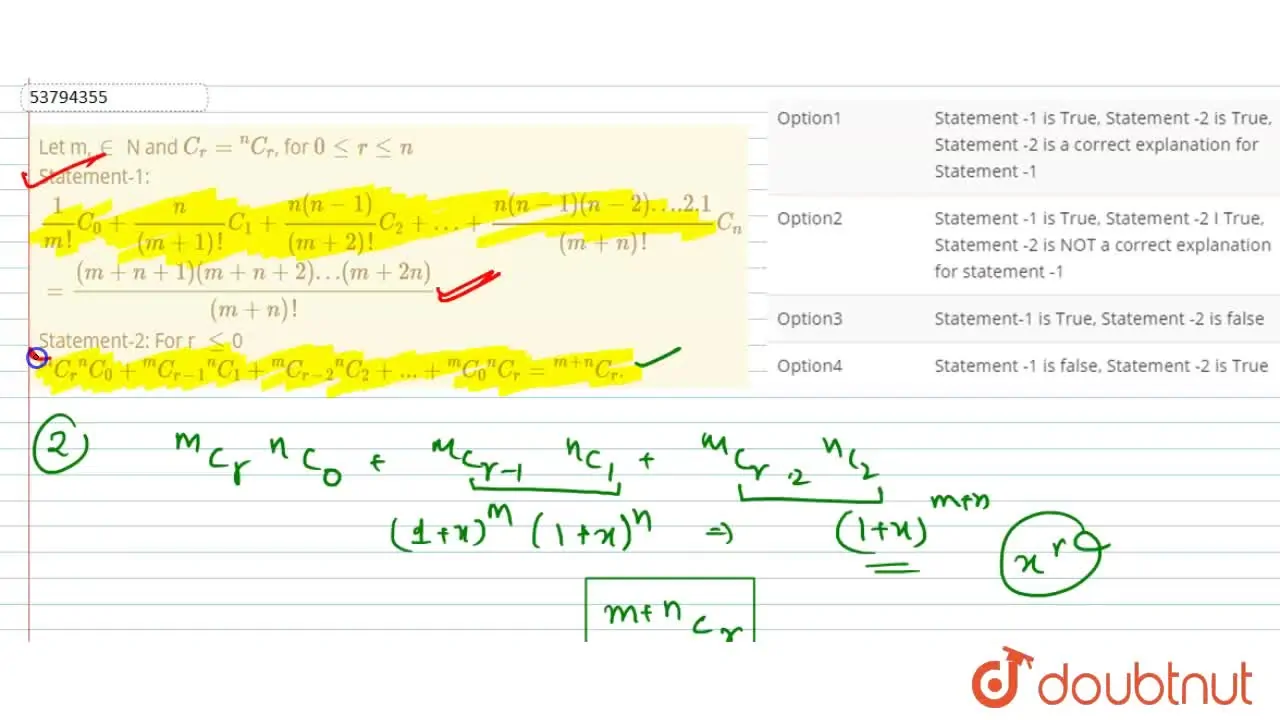
Let m,∈ N and Cr=nCr, for 0≤r≤n
Statement-1: 1m!C0+n(m+1)!C1+n(n−1)(m+2)!C2+…+n(n−1)(n−2)….2.1(m+n)!Cn
=(m+n+1)(m+n+2)…(m+2n)(m+n)!
Statement-2: For r ≤0
mCrnC0+mCr−1nC1+mCr−2nC2+...+mC0nCr=m+nCr.
A
1
B
2
C
3
D
4
Video Solution
Text Solution
The correct Answer is:a
We have,
mCrnC0+mCr−1nC1+mCr−2nC2+...+mC0nCr=m+nCr
= Coefficient of xr in {(1+x)m(1+x)n}
= Coefficient of xr in (1+x)m+n=m+nCr
So, statement-2 is true.
Now,
1m!C0+n(m+1)!C1n(n−1)(m+2)!C2+...+n(n−1)(n−2)...2.1(m+n)!Cn
=n!(m+n)!{(m+n)!m!n!nC0+(m+n)!(m+1)!(n−1)!nC1
+(m+n)!(n−2)!rC2+...+(m+n)!(m+n)!nCn}
=n!(m+n)!{m+nCn−2nC0+m+nCn−1nC1+m+nCn−2nC2+...+m+nC0nCn}
=n!(m+n)!m+n+nCn [Using statement-2]
=n!(m+n)!×(m+2n)!(m+n)!n!
=(m+n+1)(m+n+2)(m+2n)(m+n)!
So, statement-1 is also true. Statement-2 is a correct
expanation for statement-1.
|
Updated on:21/07/2023
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Exercise107videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test60videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Section I - Solved Mcqs100videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise29videos
CARTESIAN CO-ORDINATE SYSTEM
Similar Questions
Evaluate ∣∣ ∣∣mC1mC2mC3nC1nC2nC3pC1pC2pC3∣∣ ∣∣
View SolutionProve that nCr+2nCr−1+nCr−2=n+2Cr.
View SolutionIf m,n,r are positive integers such that r < m,n, then
mCr+mCr−1nC1+mCr−2nC2+...+mC1nCr−1+nCr equalsView SolutionIf m,n,r are positive integers such that r < m,n, then
mCr+mCr−1nC1+mCr−2nC2+...+mC1nCr−1+nCr equalsView SolutionThe vaule of n−1∑r=0(CrnCr+nCr+1 is equal to
View Solutionn−2Cr+2n−2Cr−1+n−2Cr−2 equals :
View Solutionn−2Cr+2n−2Cr−1+n−2Cr−2 equals :
View Solution.nC0+.n+1C1+.n+2C2…….+.nCm is equal to :
View Solution^(n)Cm+n−1Cm+n−2Cm+............+mCm
View SolutionIf n is an odd natural number and
nC0<nC1<nC2<...<nCr>nCr+1>nCr+2>...>nCn,
then r=View Solution