Let m be the smallest positive integer such that the coefficient of x2 in the expansion of (1+x)2+(1+x)3+(1+x)4+........+(1+x)49+(1+mx)50 is (3n+1).51C3 for some positive integer n. Then the value of n is
16
5
21
11
The correct Answer is:B
We find that
(1+x)2+(1+x)3+…(1+x)49+(1+mx)50
=(1+x)2{(1+x)48−1(1+x)−1}+(1+mx)50
1x{(1+x)50−(1+x)2}+(1+mx)50
Coeffi. Of x2 in (1+x)2+(1+x)3+...(1+x)49+(1+mx)50
= Coeffi.of x2 in [1x{(1+x)50−(1+x)2}+(1+mx)50]
Coeffi.ofx^(3)∈{ (1 + x)^(50) - (1 + x)(2)} + Coefficientofx^(2)∈(1 +mx)^(50)<br>""^(50)C_(3) + ""^(50)C_(2) m^(2)<br>Itisgiventˆthiscoefficientis(3n +1) ""^(51)C_(3).<br>therefore ""^(50)C_(3) + ""^(50)C_(2) m^(2) = (3n +1)""^(51)C_(3)<br>rArr (50xx49xx48)/(3xx2xx1)+(50xx49)/(2xx1)m^(2) = (3n-1)(51xx50xx49)/(3xx2xx1)<br>rArr 16 + m^(2) = 17 (3n +1)<br>rArr m^(2) = 51n+1<br>The≤∗valueofnforwhich51 N+1 is a perfect square is 5 and
for this value of n the value of m is 16.
Hence,m=16 and n=5.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Section I - Solved Mcqs100videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Section I - Assertion Reason Type13videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise29videos
CARTESIAN CO-ORDINATE SYSTEM
Similar Questions
The coefficient of xn in the expansion of 1(1−x)(3−x), is
View SolutionThe coefficient of xn in the expansion of (1+x)2(1−x)3, is
View SolutionIf n is a positive integer, then the coefficient of xn in the expansion of (1+2x)n1−x is
View SolutionFind the coefficient of xn in the expansion of 1(1−x)(1−2x)(1−3x)
View SolutionIf n is a positive integer, find the coefficient of x−1 in the expansion of (1+x)n(1+1x)n.
View SolutionIf 'n' is a positive integer then prove that the coefficient foxm in the expansion of (x2+1x)2n is :
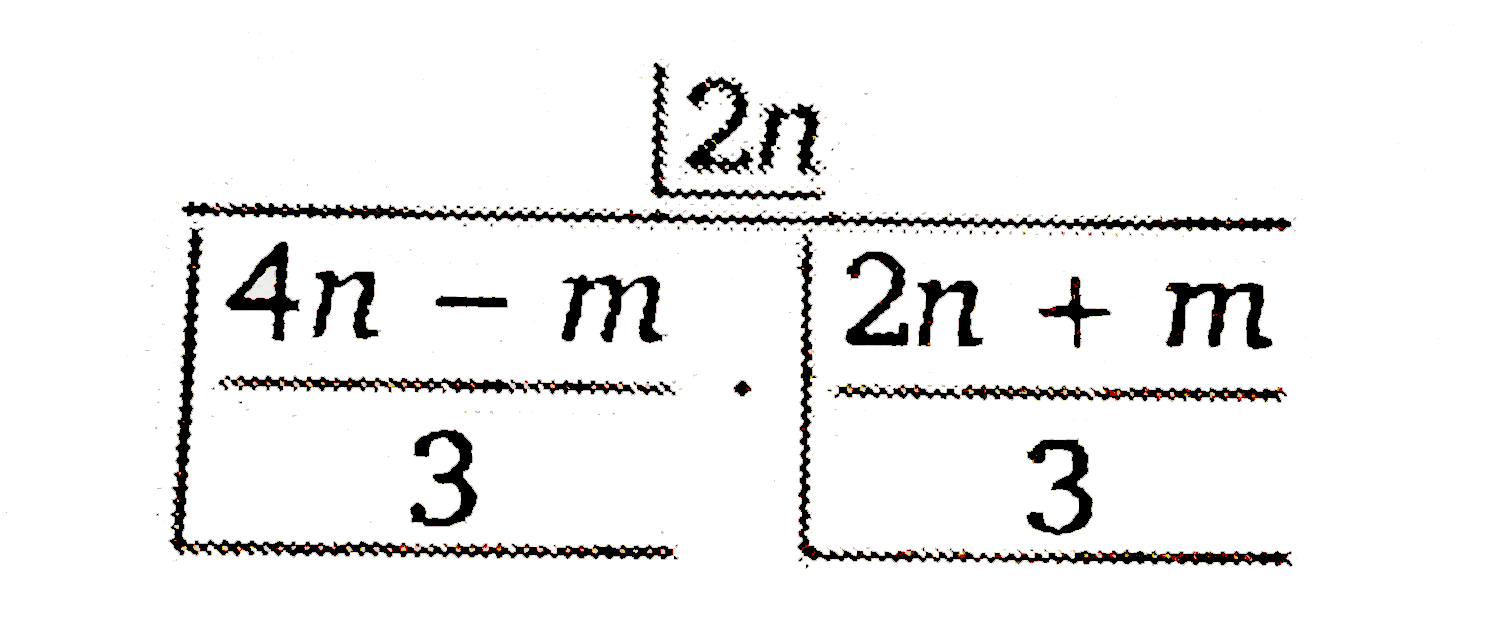 View Solution
View SolutionIf 'n' is a positive integer then prove that the coefficient foxm in the expansion of (x2+1x)2n is :
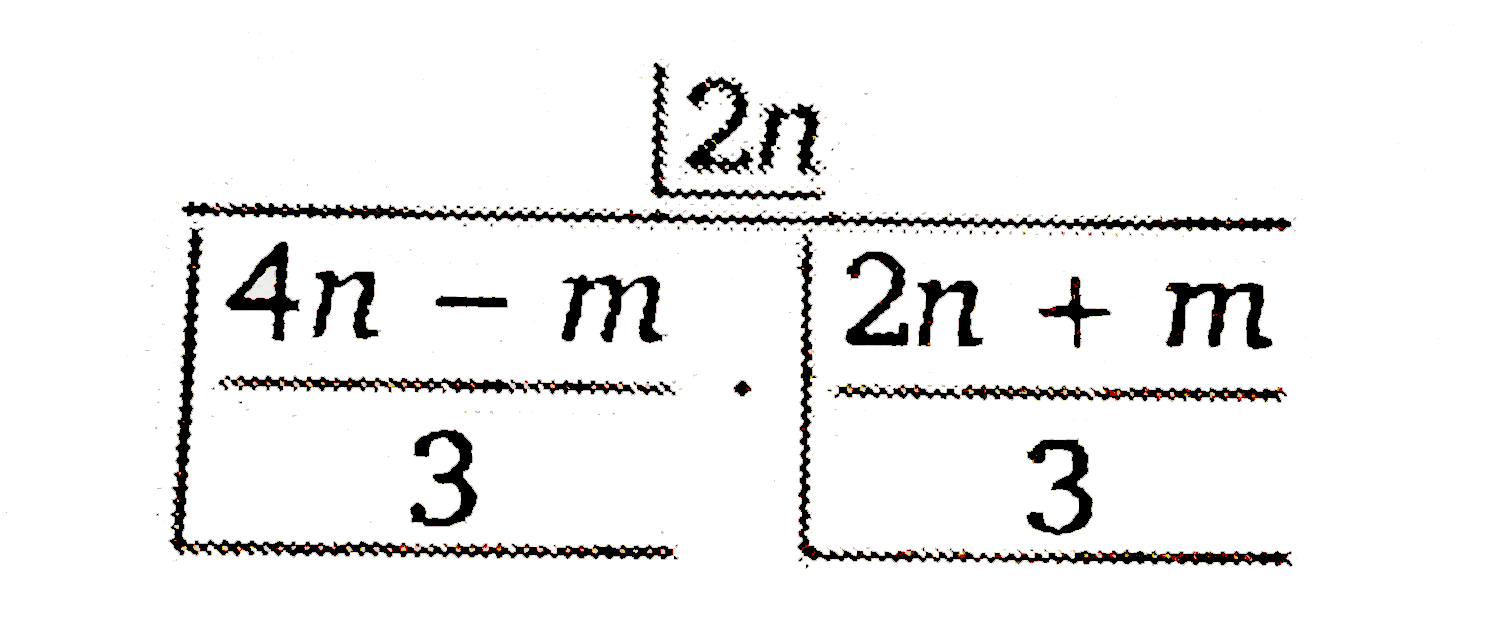 View Solution
View Solutionif n is a positive integer, find the co-efficient of xn in the expansion of (3x−2)n(1−x)2
View SolutionIf n be a positive integer, show that the algebraic sum of thenumerical coefficients in the expansion of (3x−2y)n is 1 .
View SolutionIf m and n are positive integers, then prove that the coefficients of xm and xn are equal in the expansion of (1+x)m+n
View Solution


