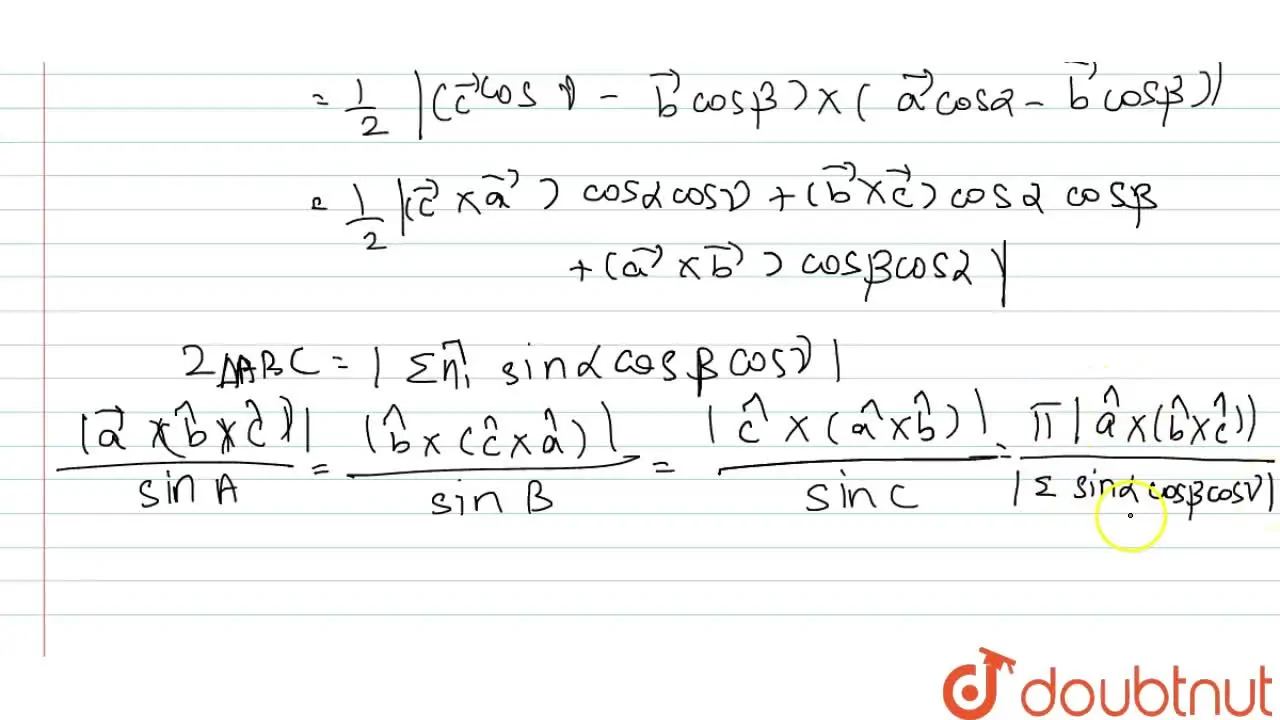Let ˆa,→band→c be the non-coplanar unit vectors. The angle between ˆbandˆcisαbetweenˆcandˆaisβandbetweenˆaandˆbisγ. If A(ˆacosα),B(ˆbcosβ)andC(ˆccosγ), then show that in triangle ABC, ∣∣ˆa×(ˆb׈ca)∣∣sinA=∣∣ˆb×(ˆc׈a)∣∣sinB=∣∣ˆc×(ˆa׈b)∣∣sinC=∏∣ˆa×(ˆ×ˆc∣)∑sinα−cosβ.cosγˆn1 where ˆn1=ˆb׈c∣∣ˆb׈c∣∣,ˆn2=ˆc׈a|ˆc׈a|andˆn3=ˆa׈b∣∣ˆa׈b∣∣Solution in Tamil
From the sine rule, we get
ABsinC=ACsinB=BCsinA=(AB)(BC)(CA)2ΔABC
BC=∣∣∣−−→BC∣∣∣=∣∣ˆccosγ=−ˆbcosβ∣∣=∣∣(ˆa.ˆb)ˆc−(ˆc.ˆa)ˆb∣∣=∣∣(ˆa×(ˆb׈c))∣∣
AC=∣∣∣−−→AC∣∣∣=∣∣ˆb×(ˆc׈a)∣∣andAB=∣∣∣−−→AB∣∣∣=ˆc×(ˆa׈b)∣∣∣
ΔABC=12∣∣∣−−→BC×−−→BA∣∣∣
=12∣∣(ˆccosγ−ˆbcosβ)×(ˆacosα−ˆbcosβ)∣∣
=12∣∣(ˆc׈a)cosαcosγ+(ˆb׈c)cosαcosβ+(ˆa׈b)cosβcosα∣∣
2ΔABC=∣∣∑ˆn1sinαcosβcosγ∣∣
∣∣ˆa×(ˆb׈c)∣∣sinA=∣∣ˆb×(ˆc׈a)∣∣sinB=∣∣ˆc×(ˆa׈b)∣∣sinC=∏∣∣ˆa×(ˆb׈c)∣∣|∑sinαcosβcosγˆn1|
Related Playlists
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise337videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DETERMINANTSEXERCISE - All Questions268videos
DETERMINANTS
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Question Bank7videos
DIFFERENTIAL EQUATIONS
Similar Questions
Find |→a|and∣∣→b∣∣, if (→a+→b)⋅(→a−→b)=8and|→a|=8∣∣→b∣∣.
05:54View SolutionStatement 1: If bc+qr=ca+rp=ab+pq=−1, then|apapbqbqcrcr|=0(abc,pqr≠0). Statement 2: if system of equations a1x+b1y+c1=0,a2x+b2y+c2=0,a3x+b2y+c3=0 has non -trivial solutions |a1b1c1a2b2c2a3b3c3|=0
02:17View SolutionFind the real value of m for which the subsititution y=um will transform the differential equation 2x4ydydx+y4=4x6 in to a homogenous equation.
View SolutionIf vectors ˆa,ˆb,ˆc are in space such that ˆa.ˆb=ˆb.ˆc=ˆc.ˆa=12, then (ˆa׈b).(ˆa×(ˆb׈c)) is equal to
View SolutionLet ˆa,ˆb and ˆc be unit vectors and α,β, and γ the angles between the vectors ˆa,ˆb,ˆb,ˆc and ˆc,ˆa respectively . If ˆa+ˆb+ˆc is also a unit vectors, then cosα+cosβ+cosγ is equal to -
View SolutionLet ˆa,→band→c be the non-coplanar unit vectors. The angle between ˆbandˆcisαbetweenˆcandˆaisβandbetweenˆaandˆbisγ. If A(ˆacosα),B(ˆbcosβ)andC(ˆccosγ), then show that in triangle ABC, ∣∣ˆa×(ˆb׈ca)∣∣sinA=∣∣ˆb×(ˆc׈a)∣∣sinB=∣∣ˆc×(ˆa׈b)∣∣sinC=∏∣ˆa×(ˆ×ˆc∣)∑sinα−cosβ.cosγˆn1 where ˆn1=ˆb׈c∣∣ˆb׈c∣∣,ˆn2=ˆc׈a|ˆc׈a|andˆn3=ˆa׈b∣∣ˆa׈b∣∣
View SolutionIf →a,→band→c are three non-coplannar vectors, then prove that ∣∣ˆa×(ˆb׈c)∣∣sinA=∣∣ˆb×(ˆc׈a)∣∣sinB=∣∣ˆc×(ˆa׈b)∣∣sinC=∏∣∣ˆa×(ˆb׈c)∣∣|∑sinαcosβcosγˆn1|
03:16View SolutionLet ˆa,→band→c be the non-coplanar unit vectors. The angle between ˆbandˆcisαbetweenˆcandˆaisβandbetweenˆaandˆbisγ. If A(ˆacosα),B(ˆbcosβ)andC(ˆccosγ), then show that in triangle ABC, ∣∣ˆa×(ˆb׈ca)∣∣sinA=∣∣ˆb×(ˆc׈a)∣∣sinB=∣∣ˆc×(ˆa׈b)∣∣sinC=∏∣ˆa×(ˆ×ˆc∣)∑sinα−cosβ.cosγˆn1 where ˆn1=ˆb׈c∣∣ˆb׈c∣∣,ˆn2=ˆc׈a|ˆc׈a|andˆn3=ˆa׈b∣∣ˆa׈b∣∣
05:25View SolutionIf →a,→band→c are three non-coplannar vectors, then prove that ∣∣ˆa×(ˆb׈c)∣∣sinA=∣∣ˆb×(ˆc׈a)∣∣sinB=∣∣ˆc×(ˆa׈b)∣∣sinC=∏∣∣ˆa×(ˆb׈c)∣∣|∑sinαcosβcosγˆn1|
02:54View SolutionIf ˆa,ˆb,ˆc are three units vectors such that ˆb and ˆc are non-parallel and ˆa×(ˆb׈c)=1/2ˆb then the angle between ˆa and ˆc is
07:29View SolutionIf ˆa,ˆbandˆc are non-coplanar unti vectors such that [ˆaˆbˆc]=[ˆb׈c ˆc׈a ˆa׈b], then find the projection of ˆb+ˆc on ˆa׈b .
02:54View Solutionˆa,ˆb,ˆc என்ற மூன்று அலகு வெக்டர்களில் b, c என்பன இணை அல்லாத வெக்டர்கள் மற்றும் ˆa×(ˆb׈c)=12ˆbஎனில், ˆa மற்றும் ˆc என்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம் காண்க.
09:20View SolutionIf →a,→band→c are three non-coplannar vectors, then prove that ∣∣ˆa×(ˆb׈c)∣∣sinA=∣∣ˆb×(ˆc׈a)∣∣sinB=∣∣ˆc×(ˆa׈b)∣∣sinC=∏∣∣ˆa×(ˆb׈c)∣∣|∑ˆn1sinαcosβcosγ|
02:11View SolutionLet hata,hatb,hatc be unit vectors. Suppose that and the angle between hata*hatb = hata*hatc = 0 and the angle between hatb and hatc is pi/6.
03:39View SolutionIf ˆa,ˆbandˆc are non-coplanar unti vectors such that [ˆaˆbˆc]=[ˆb׈c ˆc׈a ˆa׈b], then find the projection of ˆb+ˆc on ˆa׈b .
06:09View Solution