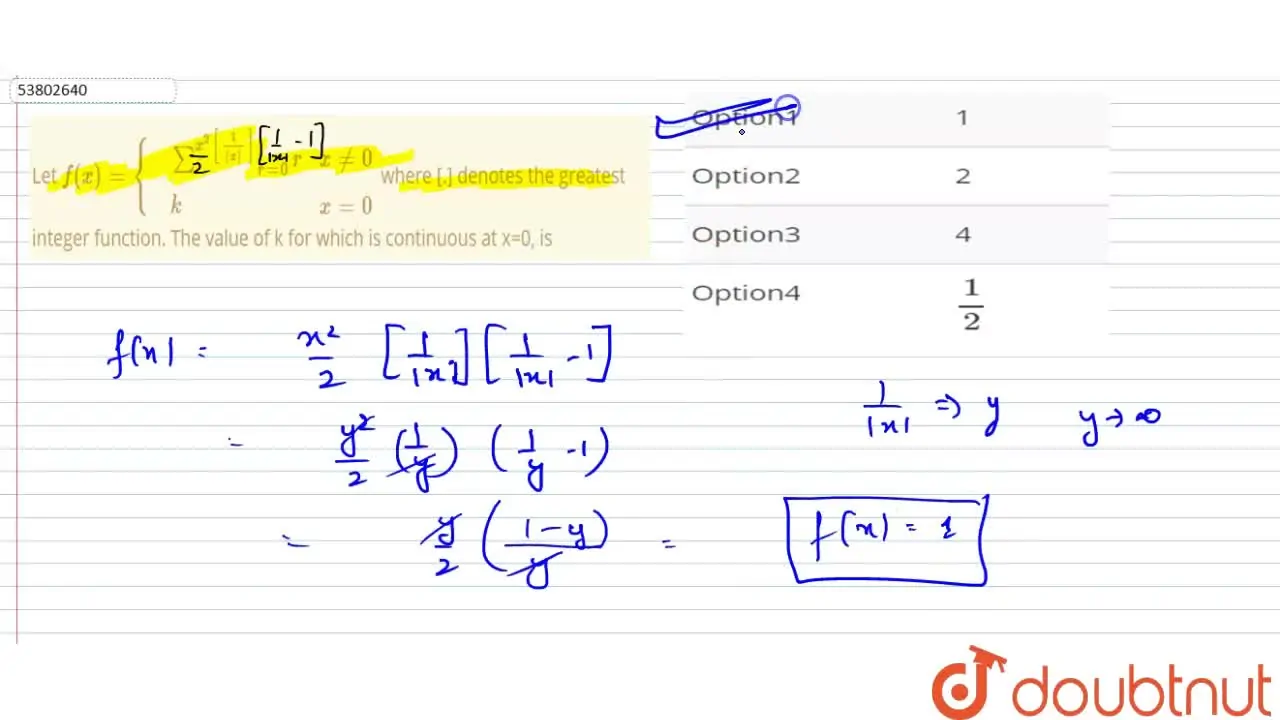
Let where [.] denotes the greatest integer function. The value of k for which is continuous at x=0, is
1
2
4
The correct Answer is:A
Clearly, f(x) is an even function and is given by
If f is continous at x=0, then
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
Similar Questions
iff(x)={2x−[x]+sin(x−[x])x≠00x−0 where [.] denotes the greatest integer function then
View SolutionIf f(x)=[x]|x|,x≠0, where [.] denotes the greatest integer function, then f'(1) is
View SolutionIf f(x)=[x]|x|,x≠0 where [.] denotes the greatest integer function, then f'(1) is
View SolutionLet f(x)=⎧⎨⎩xe[x]+x−4[x]+|x|x≠03x=0
Where [ ] denotes the greatest integer function. Then,View SolutionIf f(x)={gx,x<0anda[x],a∈R−{0},x≥0, where [.] denotes the greatest integer function. The f(x)
View SolutionLet f(x)={x[1x]+x[x]ifx≠00ifx=0 (where [x] denotes the greatest integer function). Then the correct statement is/are
View SolutionLet f(x)={81x,x<0a[x],a∈R−{0},x≥0 (where [.] denotes the greatest integer function).
Then f(x) isView SolutionIf [log2(x[x])]≥0. where [.] denotes the greatest integer function, then :
View SolutionIf f(x)=⎧⎨⎩e|x|+|x|−1|x|+|x|:x≠0−1:x=0 (where [.] denotes the greatest integer integer function), then
View Solutionf(x)=1+[cosx]x, in 0≤x≤x2 (where [.] denotes greatest integer function)
View Solution