Question

Let $f\left(x\right)=\left|\sin x\right|$
. Then,
(a) $f\left(x\right)$
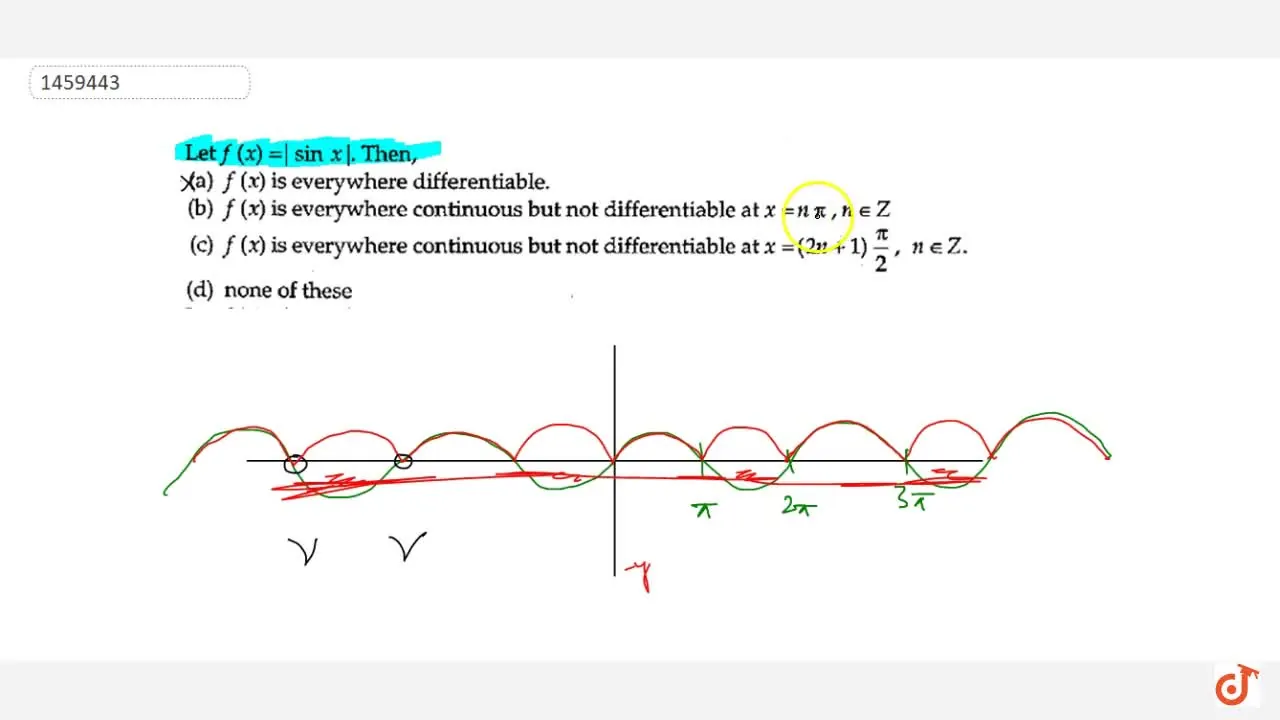
is everywhere
differentiable.
(b) $f\left(x\right)$
is everywhere
continuous but not differentiable at $x=n\pi ,n\in Z$

(c) $f\left(x\right)$
is everywhere
continuous but not differentiable at $x=(2n+1)\frac{\pi }{2}$
, $n\in Z$
.
(d) none of these

Explanation

To solve the problem, we need to analyze the function $$f\left(x\right)=|\sin x|$$ and determine its differentiability and continuity at various points.

1. Understanding the Function:
The function \( f(x) = |\sin x| \) takes the sine function and reflects any negative values above the x-axis. This means wherever \( \sin x \) is negative, \( f(x) \) will be positive.

2. Graphing the Function:
- The graph of \( \sin x \) oscillates between -1 and 1.
- The graph of \( |\sin x| \) will have peaks at \( 1 \) and troughs at \( 0 \) (where \( \sin x \) crosses the x-axis).

3. Identifying Points of Non-Differentiability:
- The points where \( \sin x = 0 \) are \( x = n\pi \) for \( n \in \mathbb{Z} \) (where \( n \) is any integer).
- At these points, the graph of \( |\sin x| \) has corners (or cusps) because the slope changes abruptly from negative to positive as it crosses the x-axis.

4. Checking Continuity:
- The function \( f(x) = |\sin x| \) is continuous everywhere since the sine function is continuous, and the absolute value function does not introduce any discontinuities.

5. Differentiability:
- The function is differentiable everywhere except at the points \( x = n\pi \) where it has corners.
- At these points, while the function is continuous, the derivative does not exist due to the abrupt change in direction.

6. Conclusion:
- Therefore, the function \( f(x) \) is continuous everywhere but not differentiable at \( x = n\pi \) for \( n \in \mathbb{Z} \).
- The correct answer is (b): \( f(x) \) is everywhere continuous but not differentiable at \( x = n\pi, n \in \mathbb{Z} \).