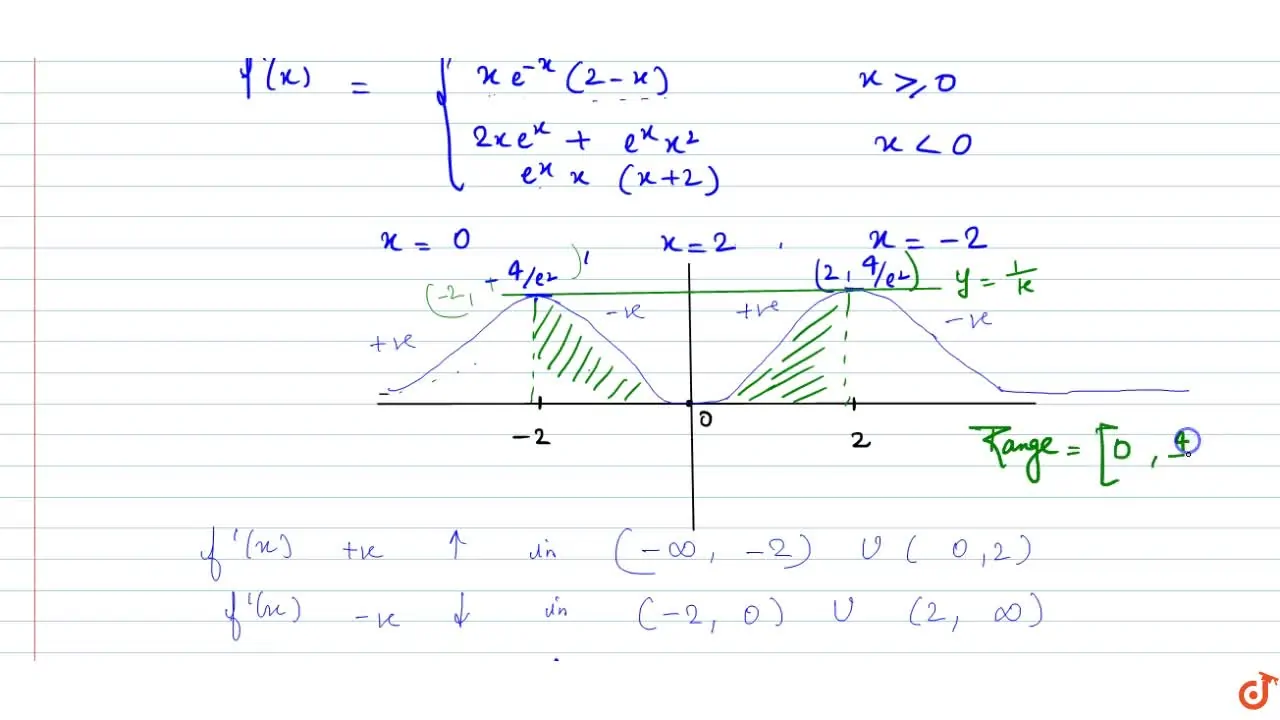
Let be a real valued continuous function on defined as The value of for which the curve intersect the curve at exactly two points, is (b) (c) (d)
The correct Answer is:A, D
Graph of 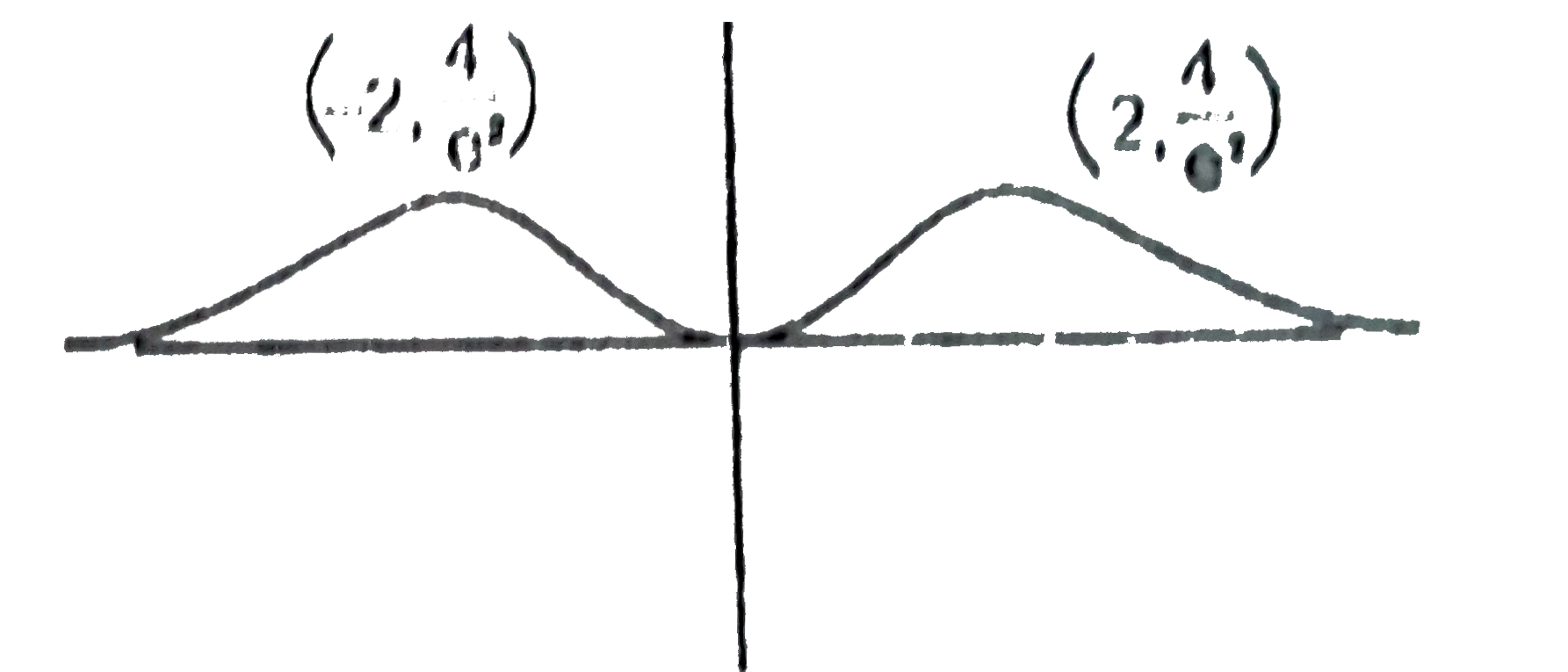
will intersect
Then
Related Playlists
Similar Questions
Let f(x) be a real valued continuous function on R defined as f(x)=x2e−|x| The value of k for which the curve y=kx2(k>0) intersect the curve y=e|x| at exactly two points, is e2 (b) e22 (c) e24 (d) e28
View SolutionLet f(x) be real valued continuous function on R defined as f(x)=x2e−|x| then f(x) is increasing in
View SolutionLet f(X) be real valued continous funcion on R defined as f(X) =x2e−|x|
The values of k for which the equation x2e−|x|=k has four real roots areView Solutionlet f:R→R be a continuous function defined by f(x)=1ex+2e−x
View SolutionLet f be a real valued function defined by f(x)=ex−e−|x|ex+e|x| , then the range of f(x) is: R (b) [0,1] (c) [0,1) (d) [0,12)
View SolutionLet the function f(x) be defined as f(x)={logx−1x−ex≠ekx=e
The value of k , for which the function is continuous at x =e , is equal toView SolutionLet f be a real valued function defined by f(x)=ex−e−|x|ex+e|x| , then the range of f(x) is: (a)R (b) [0,1] (c) [0,1) (d) [0,12)
View SolutionIf the curves y=2 ex and y=ae−x intersect orthogonally, then a= 1/2 (b) −1/2 (c) 2 (d) 2e2
View SolutionThe function f:R+→(1,e) defined by f(x)=x2+ex2+1 is
View SolutionLet f:R→R be a function defined by f(x)=e|x|−e−xex+e−x, then f(x) is
View Solution