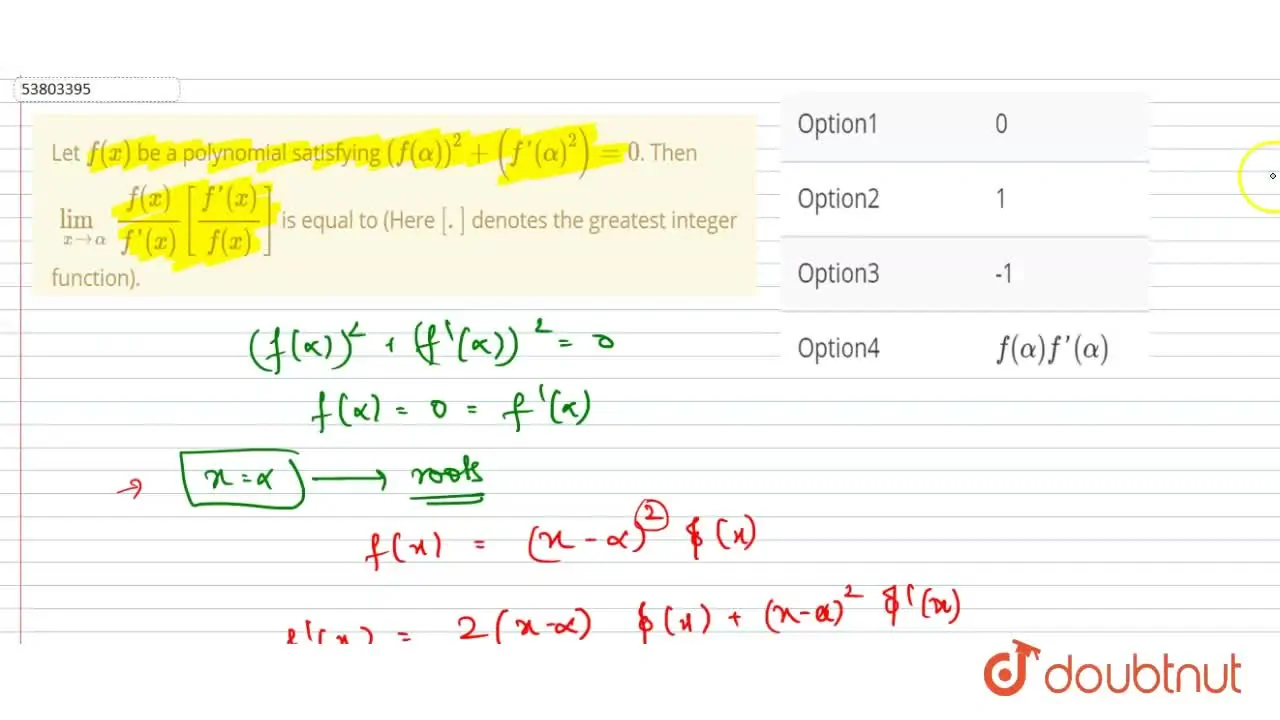
Let f(x) be a polynomial satisfying (f(α))2+(f'(α)2)=0. Then limx→αf(x)f'(x)[f'(x)f(x)] is equal to (Here [.] denotes the greatest integer function).
0
1
-1
f(α)f'(α)
The correct Answer is:B
It is given that the polynomial f(x) satisfies the relation (f(α))2+(f'(α))2=0
∴f(α)=0=f'(α)
⇒x=α is a root of f(x) and f'(x)
⇒(x−α)2 is a foactor of f(x).
Let f(x)=(x−α)2ϕ(x). Then,
f'(x)=2(x−α)ϕ(x)+(x−α)2ϕ'(x)
∴f(x)f'(x)=(x−α)ϕ(x)2ϕ(x)+(x−α)ϕ'(x)
Now, limx→αf(x)f(x)[f'(x)f(x)]
limx→αf'(x)f'(x)(f'(x)f'(x)−{f(x)f(x)}), whwre [.] denotes the fractional part function.
=limx→αf(x)f(x)×f'(x)f(x)−limx→αf(x)f'(x){f'(x)f(x)}
=1−limx→αx−α2ϕ(x)+(x−α)ϕ'(x)
{2ϕ(x)+(x−α)ϕ'(x)(x−α)ϕ(x)}
=10=1.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Section II - Assertion Reason Type5videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Exercise99videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Chapter Test60videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test30videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise30videos
MATHEMATICAL INDUCTION
Similar Questions
Let f(x)=(−1)[x] where [.] denotes the greatest integer function), then
View SolutionIf f(x)=[|x|], then ∫1000f(x)dx is equal to (where [.] denotes the greatest integer function)
View SolutionIf f(x)=[x]|x|,x≠0, where [.] denotes the greatest integer function, then f'(1) is
View SolutionGiven limx→0f(x)x2=2, where [.] denotes the greatest integer function, then
View SolutionIf f(x)=[x]|x|,x≠0 where [.] denotes the greatest integer function, then f'(1) is
View SolutionLet f(x)=[sinxx],x≠0 , where [.] denotes the greatest integer function then limx→0f(x)
View SolutionIff(x)={x+12,x<02x+34,x≥0 , then [(lim)x→0f(x)]= (where [.] denotes the greatest integer function)
View SolutionLet f(x) be a polynomial satisfying f(0)=2 , f'(0)=3 and f''(x)=f(x) then f(4) equals
View SolutionIf f(x)=cos|x|+[∣∣∣sinx2∣∣∣], (where [.] denotes the greatest integer function), then f(x) is
View SolutionLet f(x)=tanxx, then loge(limx→0([f(x)]+x2)1{f(x)}) is equal, (where [.] denotes greatest integer function and {.} fractional part)
View Solution