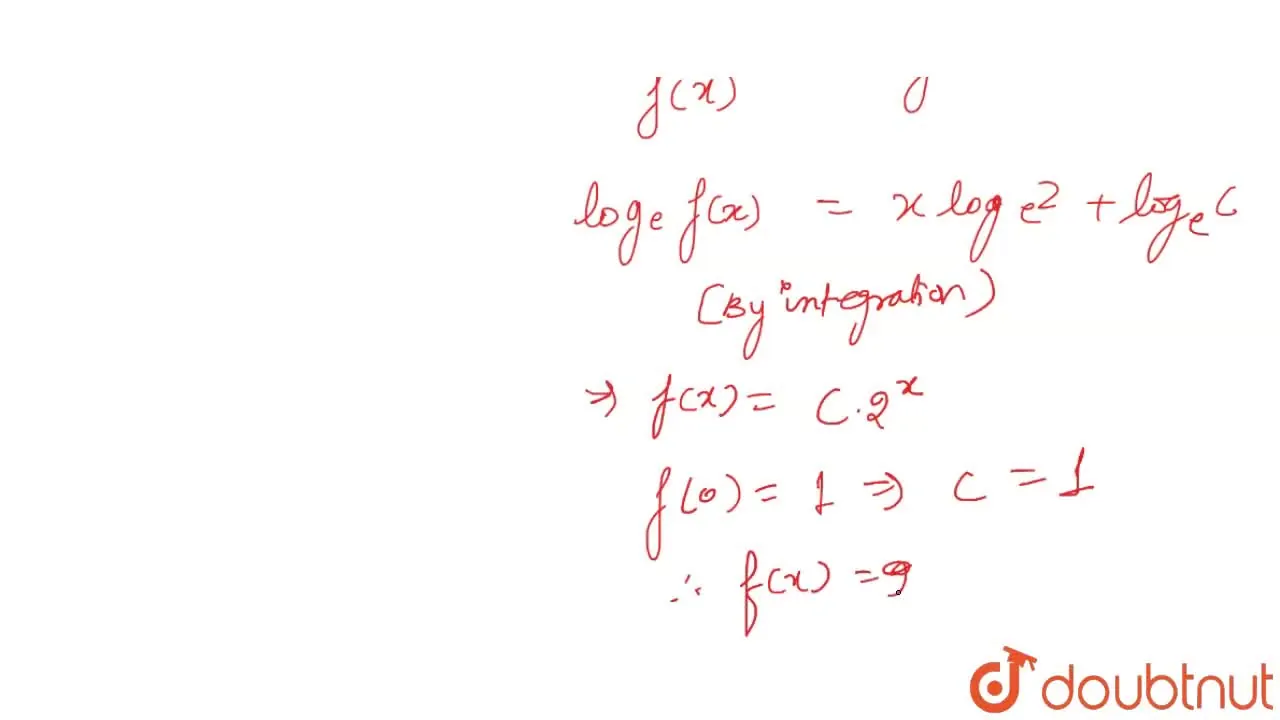Let f:R∈R be a function given by f(x+y)=f(x)f(y)for allx,y∈R
If (x)≠0,for all x∈Randf'(0)=log2,then f(x)=
x2
2x
x(log2)
e2x
The correct Answer is:B
Proceeding as in Example 33, we have
f'(x)=f(x).loge2
⇒f'(x)f(x)=loge2
⇒logef(x)=xloge2+logeC [On integrating]
⇒f(x)=C2x<br>"But "f(0)=1"Therefore "C=1<br>Hence,f(x)=2^(x)
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
Similar Questions
Let f:R→R be a function given by
f(x+y)=f(x)f(y) for all x,y∈R
If f(x)≠0 for all x∈R and f'(0) exists, then f'(x) equalsView SolutionLet f:R→R be a function given by f(x+y)=f(x)f(y) for all x,y∈ R .If f'(0)=2 then f(x) is equal to
View SolutionLet f:R→R be a function given by f(x+y)=f(x)+f(y) for all x,y ∈R such that f(1)=a Then, f(x)=
View SolutionLet f:R→R be a function given by
f(x+y)=f(x)f(y)for all x,y∈R
If f(x)=1+xg(x),loge2,where limx→0g(x)=1.Then,f'(x)=View SolutionLet f:R→R be a function such that f(x+y)=f(x)+f(y),∀x,y∈R.
View SolutionLet f:R→R be a function satisfying f(x+y)=f(x)+f(y)for all x,y∈R
If f(x)=x3g(x)for all x,y∈R, where g(x) is continuous, then f'(x) is equal toView SolutionLet f:R→R be given by f(x+y)=f(x)−f(y)+2xy+1for all x,y∈R If f(x) is everywhere differentiable and f'(0)=1, then f'(x)=
View SolutionLet f:R→R be a function satisfying condition f(x+y3)=f(x)+[f(y)]3forallx,y∈R. If f′(0)≥0, find f(10).
View SolutionLet f:r∈R be a contunuous function given be f(x+y)=f(x)+f(y)for all x,by∈R.
If ∫20f(x)dx=α,then∫22f(x)dx is equal toView SolutionLet f:R→R be a function such that f(x+y)=f(x)+f(y)for all,x,y∈R
If f(x) is differentiable at x=0. then, which one of the following is incorrect?View Solution