Let f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] 4satisfying the equation f(x)=10−x10 is
The correct Answer is:3
f:[0,4π]→[0,π],f(x)=cos−1(cosx)
For number of roots of equation cos−1(cosx)=10−x10, draw the graph of y=cos−1(cosx)
and y=10−x10 and find the points of intersection.
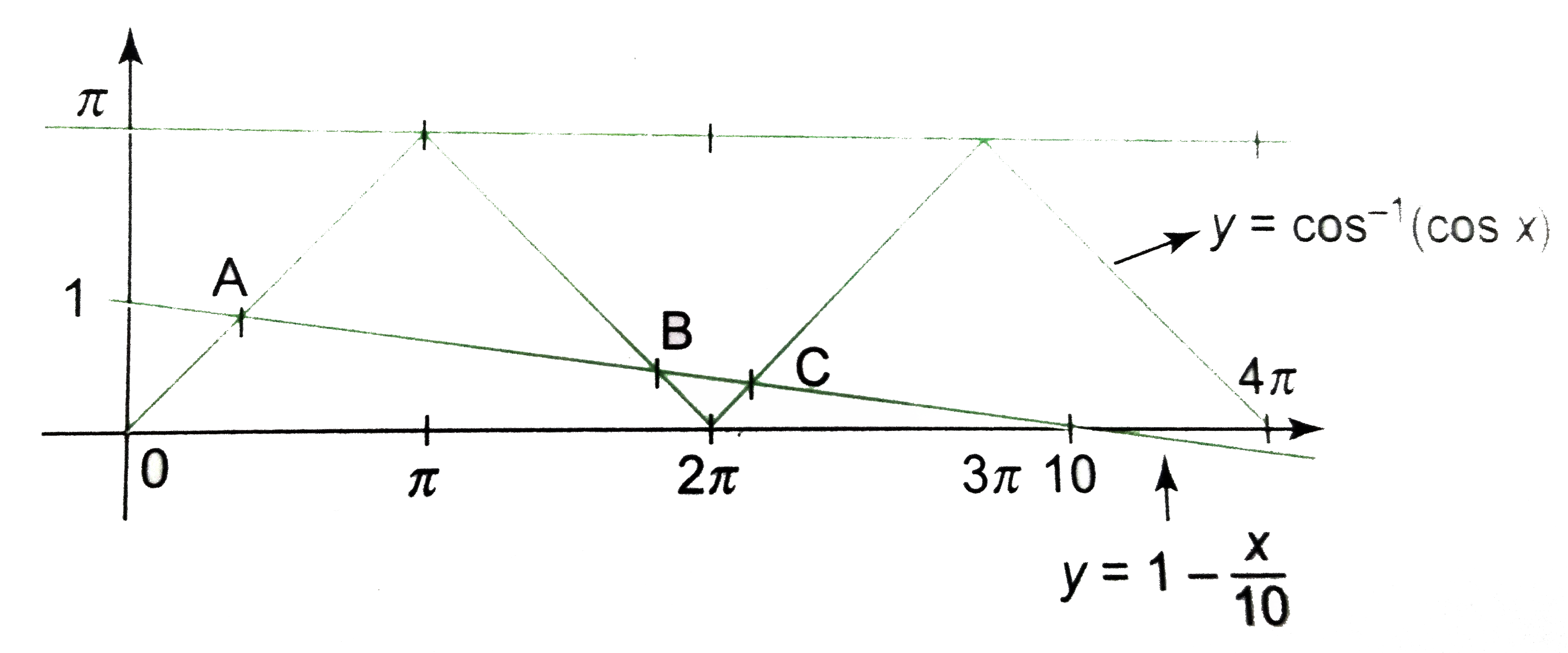
From the graph number of solution is 3
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Multiple correct answer type)2videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE3videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
Let F:[3,∞]→[1,∞] be defined by f(x)=πx(x−3), if f−1(x) is inverse of f(x) then the number of solution of the equation f(x)=f−1(x) are
View SolutionLet f(x)=max{tanx,cotx}. Then the number of roots of the equation f(x)=12 in (0,2π) is
View SolutionLet f(x)=sin23x−cos22xandg(x)=1+12tan−1|x| . Then the number of values of x in the interval [−10π,8π] satisfying the equation f(x)=sgn(g(x)) is __________
View SolutionLet f(x)=sin23x−cos22xandg(x)=1+12tan−1|x| . Then the number of values of x in the interval [−10π,8π] satisfying the equation f(x)=sgn(g(x)) is __________
View SolutionLet f:{−π2, π2}→R be a function defined by f(x)=cos[x]. Write range (f) .
View SolutionThe number of points of discontinuity for f(x) = sgn(sin x), x∈[0,4π] is ___________.
View SolutionLet a function f:R→R be defined as f(x)=x+sinx. The value of ∫2π0f−1(x)dx will be:
View SolutionConsider a function f defined by f(x)=sin−1sin(x+sinx2)∀x∈[0,π]which satisfies f(x)+f(2π−x)=π∀x∈[π,2π] and f(x)=f(4π−x)for all x∈[2π,4π] then If α is the length of the largest interval on which f(x) is increasing, then α =
View SolutionLetf(x)=max{tanx,cotx] then number of roots of equation the interval [0,2π] satisfying f(x)=1√3 is (A) 2(B) 4(C) 0 (D) infinte
View SolutionIf f(x)=cos−1(sinx(4cos2x−1)), then 1πf'(π3).f(π10) is
View Solution


