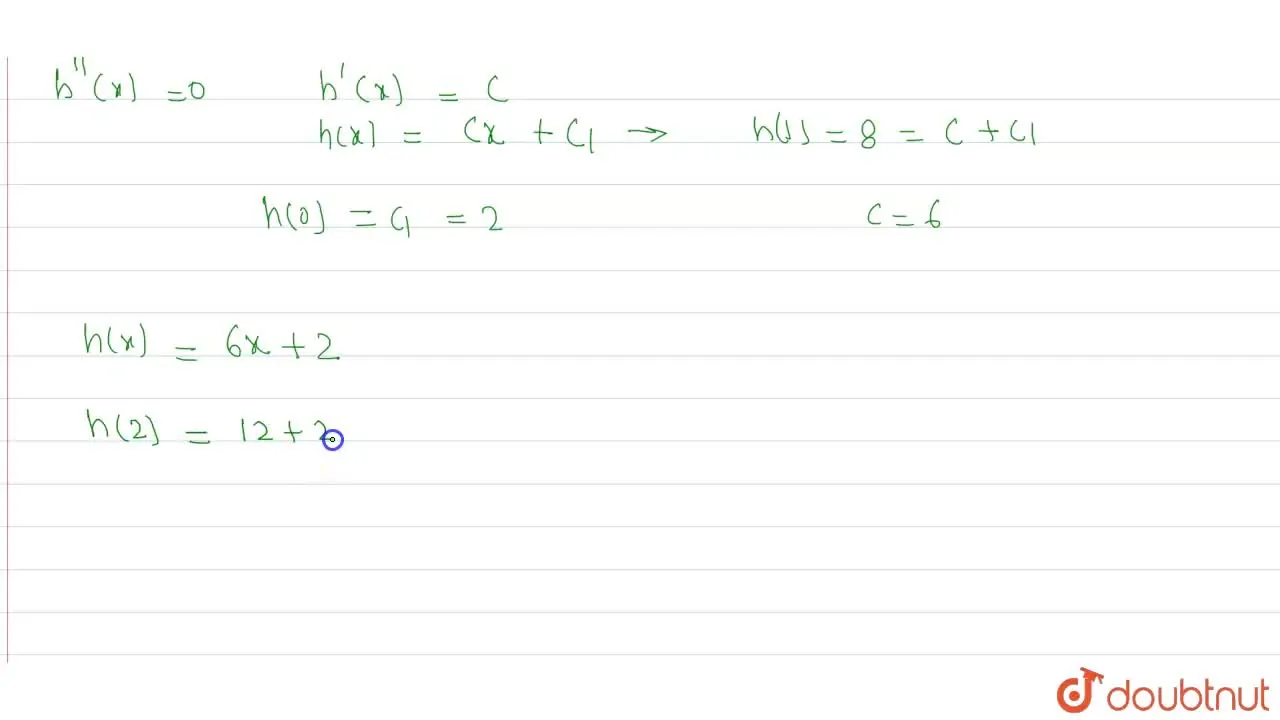Let f be a twice differentiable function such that
f''(x)=−f(x) and f'(x)=g(x).If h'(x)=[f(x)]2+[g(x)]2,
h(a)=8 and h(0)=2, then h(2)=
1
2
3
none of these
The correct Answer is:D
We have, h'(x)=[f(x)]2+[g(x)]2
⇒ h''(x)=2f(x)f'(x)+2g(x)g'(x)
⇒ h''(x)=2f(x)g(x)+2g(x)f''(x) [∵g(x)−f'(x)∴g'(x)=f'(x)]
⇒ h''(x)=2f(x)g(x)+2g(x)(−f(x)) [∵f''(x)=−f(x)]
⇒ h''(x)=0
⇒ h'(x)=c,a constant for all x∈R.
⇒ h(x)=cx+c1
⇒ h(0)=c1 and h(1)=c+c1
⇒ 2=c1 and 8=c+c1
⇒ c1=2 and c=6
∴ h(x)=6x+2⇒h(2)=6×2+2=14
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIATIONEXERCISE - Exercise60videos
DIFFERENTIATION
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test30videos
DIFFERENTIATION
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test30videos
DIFFERENTIATION
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Exercise17videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Chapter Test30videos
ELLIPSE
Similar Questions
Let f be a twice differentiable function such that fx=−f(x),andf′(x)=g(x),h(x)=[f(x)]2+[g(x)]2. Find h(10)ifh(5)=11
View SolutionIf f is twice differentiable function such that
f''(x)=−f(x), and f'(x)=g(x),h(x)=[f(x)]2+[g(x)]2 amd h(5)=11, then h(10)=View SolutionSTATEMENT - 1 : Let f be a twice differentiable function such that f'(x)=g(x) and f''(x)=−f(x) . If h'(x)=[f(x)]2+[g(x)]2,h(1)=8andh(0)=2⇒h(2)=14 and STATEMENT - 2 : h''(x)=0
View SolutionLet f be twice differentiable function such that g'(x)=−f(x)g(x), f'(x)=g(x)f(x), h(x)=e(f(x))2+(g(x))2+x If h(5)=e6, then h(10) is equal to
View SolutionIf f(x) is a twice differentiable function such that f''(x)=−f,f'(x)=g(x),h(x)=f2(x)+g2(x)andh(10)=10 , then h (5) is equal to
View SolutionIf f is twice differentiable such that f"(x)=-f(x) f'(x)=g(x),h'(x)=[f(x)]2+[g(x)]2andh(0)=2, h(1)=4, then the equation y=h(x) represents.
View SolutionLet f be a differentiable function such that f(0)=e2 and f'(x)=2f(x) for all x∈RIf h(x)=f(f(x)) ,then h'(0) is equal to
View SolutionLet f be a differentiable function such that f(1)=2 and f'(x)=f(x) for all x∈R. If h(x)=f(f(x)) then h'(1) is equal to
View SolutionLet f be a differentiable function such that f(1) = 2 and f'(x) = f (x) for all x∈R. If h(x)=f(f(x)), then h'(1) is equal to
View SolutionLet f(x) be a twice-differentiable function and f(0)=2. The evaluate: (lim)x→02f(x)−3f(2x)+f(4x)x2
View Solution