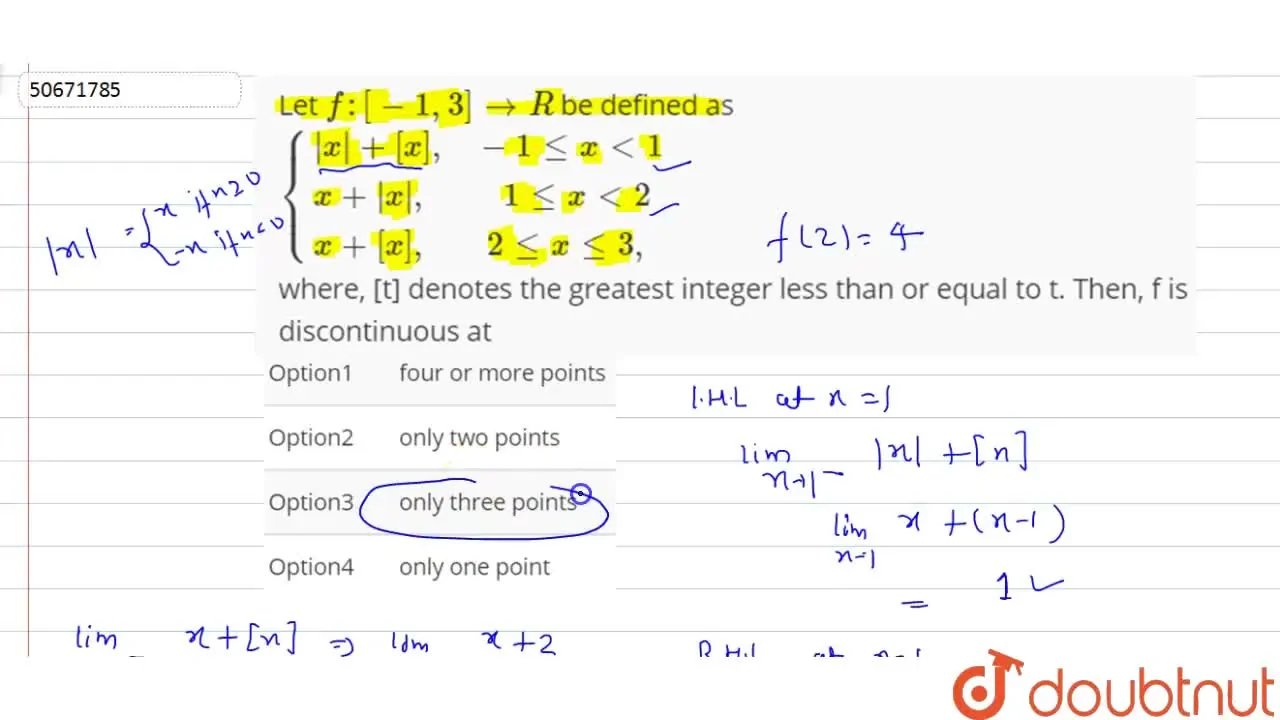
Let f:[−1,3]→R be defined as
⎧⎪⎨⎪⎩|x|+[x], −1≤x<1x+|x|, 1≤x<2x+[x], 2≤x≤3,
where, [t] denotes the greatest integer less than or equal to t. Then, f is discontinuous at
four or more points
only two points
only three points
only one point
The correct Answer is:C
Given function f:[−1,3]→R is defined as
f(x)=⎧⎪⎨⎪⎩|x|+[x], −1≤x<1x+|x|, 1≤x<2x+[x], 2≤x≤3
⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩−x−1, −1≤x<0 x, 0≤x<12x, 1≤x<2x+2, 2≤x<3 6, x=3
[∵ if n≤x<n+1,∀n∈Integer,[x]=n]
∵ limx→0−f(x)=−1≠f(0) [∵f(0)=0]
∵ limx→1−f(x)=1≠f(1) [∵f(1)=2]
∵ limx→2−f(x)=4=f(2)=limx→2+f(x)=4 [∵f(2)=4]
and limx→3−f(x)=5≠f(3) [∵f(3)=6]
∴ Function f(x) is discontinuous at points 0, 1 and 3.
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Continuity in a Domain (Objective Question II )2videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Continuity in a Domain (Fill in the Blank)1videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - (Match the Columns)1videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - JEE MAINSEXERCISE - All Questions1videos
JEE MAINS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)2videos
MATRICES AND DETERMINANTS
Similar Questions
If f(x)={x[x]0≤x<2(x−1)[x]2≤x<3 where [.] denotes the greatest integer function, then
View SolutionIf f(x)={∣∣1−4x2∣∣,0≤x<1[x2−2x],1≤x<2, where [] denotes the greatest integer function, then
View SolutionLet f(x)={x[x]0≤x<2(x−1)2≤x≤3 where [x]= greatest integer less than or equal to x, then:
The number of integers in the range of y=f(x) is:View SolutionIf f(x)=x(−1)[1x],x≤0 where [x] denotes the greatest integer less than or equal to x, then the value of limx→0f(x) is equal to:
View SolutionThe number of points where f(x)={[cosπx],0≤x≤1|2x−3|[x−2],1<x≤2
([x] is the greatest integer less than or equal to x) is discontinuous isView SolutionLet f(x)=[1/2+x]−[1/2]x , −1≤x≤2 and f(0) =0([x] is greatest integer less than or equal to x) then
View SolutionLet f(x)={x[x]0≤x<2(x−1)2≤x≤3 where [x]= greatest integer less than or equal to x, then:
The number of values of x for x∈[0,3] where f(x) is dicontnous is:View SolutionIf f(x)=⎧⎪⎨⎪⎩3, if 0≤x≤14, if 1<x<35, if 3≤x≤10, then
View SolutionIf f(x)={x−1, for 1≤x<22x+3, for 2≤x≤3, then at x=2
View Solutionf(x) is defined as f(x)=⎧⎪⎨⎪⎩|x|+[x]−1<x<1x+|x|1≤x<2|x|[x]2≤x<3
then the number of points of dicontinuity of f(x) isView Solution