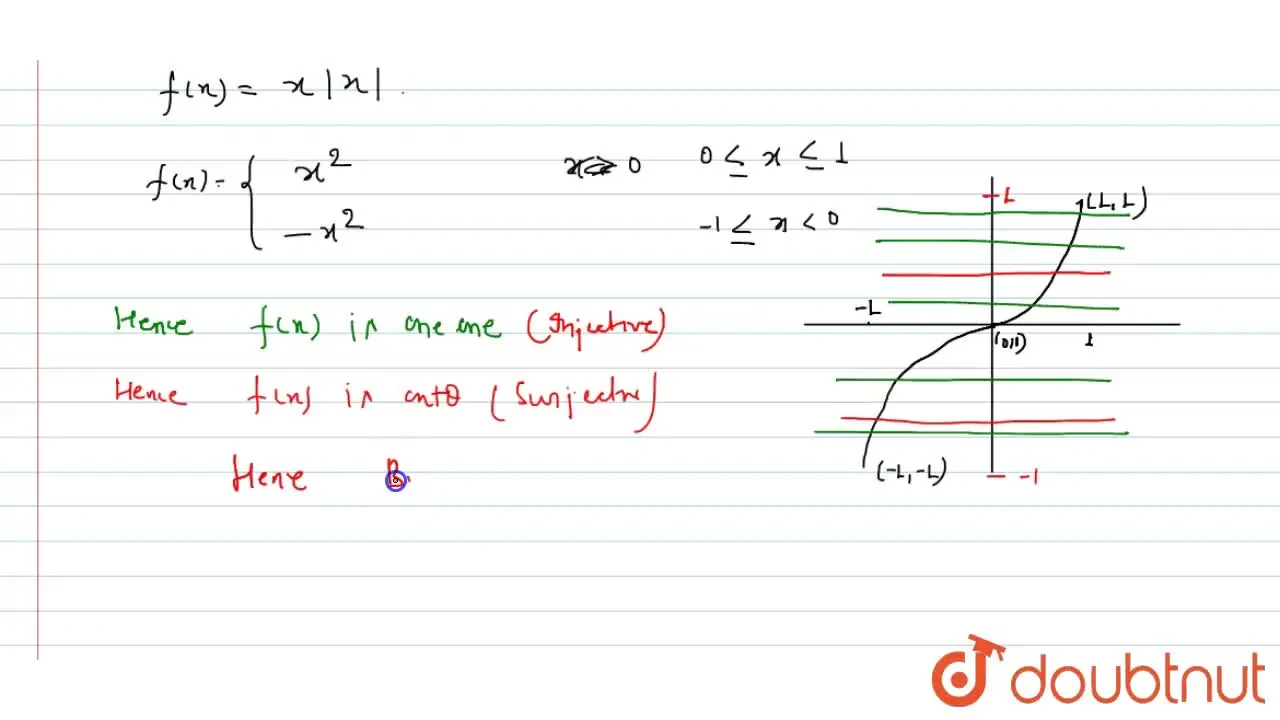
Let A={x∈R:−1≤x≤1}=B . Then, the mapping f:A→B given by f(x)=x|x| is (a) injective but not surjective (b) surjective but not injective (c) bijective (d) none of these
Injectivity :
⇒ Let {x}1 and {x}2 be any two elements in the domain {A}.
CaseI:
Let {x}1 and {x}2 be two positive numbers, such that
⇒{f}({x}1)={f}({x}2)
⇒{x}1∣∣{x}1∣∣={x}2∣∣{x}2∣∣
⇒{x}1({x}1)={x}2({x}2)
⇒{x}21={x}22
⇒{x}1={x}2
Case II:
Let {x}1 and {x}2 be two negative numbers, such that
⇒{f}({x}1)={f}({x}2)
⇒{x}1∣∣{x}1∣∣={x}2∣∣{x}2∣∣
⇒{x}1(−{x}1)={x}2(−{x}2)
⇒−{x}21=−{x}22
⇒{x}1={x}2
Case III :
Let x1 be positive and x2 be negative.
Then, {x}1≡{x}2
Rightarrow {f}({x}_{1})={x}_{1}|{x}_{1}| text { be positive and } {f}({x}_{2})={x}_{2}|{x}_{2}| text { is negative. }
⇒{f}({x}1)≡{f}({x}2)
So, {x}1≡{x}2
⇒{f}({x}1)≡{f}({x}2)
From the 3 cases, we can conclude that f is one-one.
Surjectivity :
Let y be an element in the co-domain, such that y=f(x).
Case - I :
Let y>0. Then, 0<y≤1
⇒{y}={f}({x})={x}|{x}|>0 ⇒{x}>0 ⇒|{x}|={x} ⇒{f}({x})={y} ⇒{x}|{x}|={y} ⇒{x}2={y} ⇒{x}=√{y}∈{A}( We do not get-because {x}>0)
Case II :
Let y<0. Then, −1≤y<0
⇒y=f(x)=x|x|<0
⇒|x|=−x
f(x)=y
⇒x|x|=y
⇒x(−x)=y
⇒−x2=y
⇒x2=−y
⇒{x}=−√−{y}∈{A}( We do not get + because {x}<0 )
∴{f} is onto.
Related Playlists
Similar Questions
The function f:R→R , f(x)=x2 is (a) injective but not surjective (b) surjective but not injective (c) injective as well as surjective (d) neither injective nor surjective
View Solutionf:R→R given by f(x)=x+√x2 is (a) injective (b) surjective (c) bijective (d) none of these
View SolutionLet A}x:−1≤x≤1}andf:A→ such that f(x)=x|x|, then f is a bijection (b) injective but not surjective Surjective but not injective (d) neither injective nor surjective
View SolutionLet R be the set of real numbers. If f:R→R is a function defined by f(x)=x2, then f is injective but not surjective surjective but not injective bijective none of these (a) injective but not surjective (b) surjective but not injective (c) bijective (d) non of these
View SolutionLet R be set of real numbers. If f:R→R is defined by f(x)=ex, then f is: (a) surjective but not injective (b) injective but not surjective (c) bijective (d) neither surjective nor injective.
View SolutionLet f:R→R & f(x)=x1+|x| Then f(x) is (1) injective but not surjective (2) surjective but not injective (3) injective as well as surjective (4) neither injective nor surjective
View SolutionThe mapping f:R→R given by f(x)=x3+ax2+bx+c is bijection if
View SolutionA function f:(0,∞)→[0,∞] is given by f(x)=∣∣∣1−1x∣∣∣ , then f(x) is (A) Injective but not surjective (B) Injective and bijective (C) Injective only (D) Surjective only
View SolutionLet A={x:xεR−}f is defined from A→R as f(x)=2xx−1 then f(x) is (a) Surjective but nor injective (b) injective but nor surjective (c) neither injective surjective (d) injective
View SolutionShow that f:R→R defined by f(x)=(x−1)(x−2)(x−3) is surjective but not injective.
View Solution