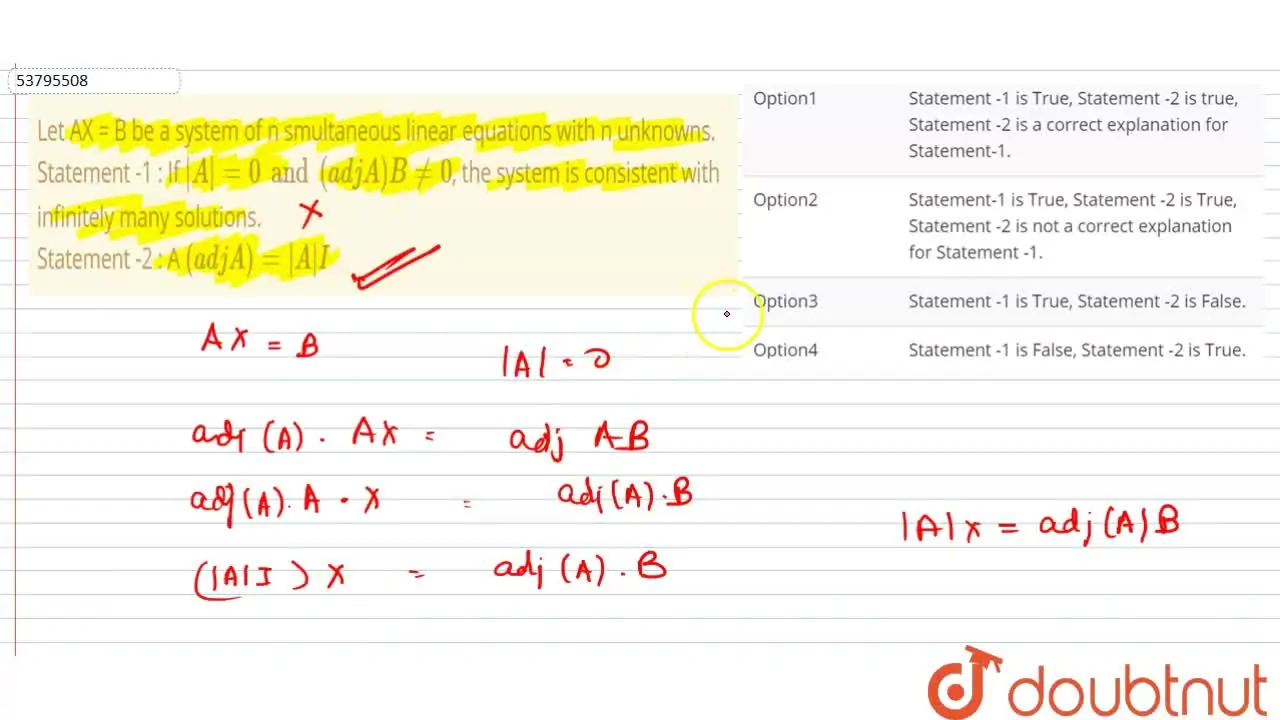
Let AX = B be a system of n smultaneous linear equations with n unknowns.
Statement -1 : If |A|=0and(adjA)B≠0, the system is consistent with infinitely many solutions.
Statement -2 : A (adjA)=|A|I
Statement -1 is True, Statement -2 is true, Statement -2 is a correct explanation for Statement-1.
Statement-1 is True, Statement -2 is True, Statement -2 is not a correct explanation for Statement -1.
Statement -1 is True, Statement -2 is False.
Statement -1 is False, Statement -2 is True.
The correct Answer is:D
We have , AX = B, where |A|=0
⇒(adjA)(AX)=(adjA)B
⇒((adjA)A)X=(adjA)B
⇒(|A|I)X=(adjA)B[f∵A(adjA)=|A|I]
⇒|A|X−(adjA)B
Clearly, it is not true when |A|=0and(adjA)B≠0,. So, the system is inconsistent.
Hence, stetement -2 is true and statement -1 is false.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATRICESEXERCISE - Exercise80videos
MATRICES
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATRICESEXERCISE - Chapter Test30videos
MATRICES
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATRICESEXERCISE - Section I - Solved Mcqs57videos
MATRICES
- BOOK - OBJECTIVE RD SHARMACHAPTER - LOGARITHMSEXERCISE - Chapter Test21videos
LOGARITHMS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise28videos
MEAN VALUE THEOREMS
Similar Questions
Let AX=B be a system of n-linear equations in n-unknowns ( in the usual notation ) such that A is a non singular matrix , then the system is consistent and has a unique solution given by
View SolutionThe system AX = B of n equation in n unknown has infinitely many solutions if
View Solutionx+ay=0,y+az=0,z+ax=0 The value of a for which the system of equations has infinitely many solutions is
View SolutionA homogenous system of 3 equation with 3 unknowns AX=0 has infinitely many solutions, if
View SolutionA homogenous system of 3 equation with 3 unknowns AX=O has infinitely many solutions, if
View SolutionThe system of equations x+py=0,y+pz=0andz+px=0 has infinitely many solutions for
View SolutionIf am= bl, then find whether the pair of linear equations ax+by=candlx+my=n has no solution, unique solution or infinitely many solutions
View SolutionThe system of linear equations ax+by=0,cx+dy=0, has a non trivial solution if
View SolutionA non-Homogeneous system of 3 equations in three unknowns AX=D has infinitely many solutions, if
View SolutionIf the system of simultaneous linear equations x+y+z=a, x−y+bz=2, 2x+3y−z=1 has infinitely many solutions,then b−5a=
View Solution