Let A=⎡⎢⎣tanπ3sec2π3cot(2013π3)cos(2012π)⎤⎥⎦ and P be a 2×2 matrix such that PPT=I, where I is an identity matrix of order 2. If Q=PAPT and R=[rij]2×2=PTQ8P, then find r11.
R=PTQ8P
=PT(PAPT)8P
=PTPAPT(PAPT)7P
=IAPT(PAPT)7P
=APTPAPT(PAPT)6P
=A2PT(PAPT)6P
...
...
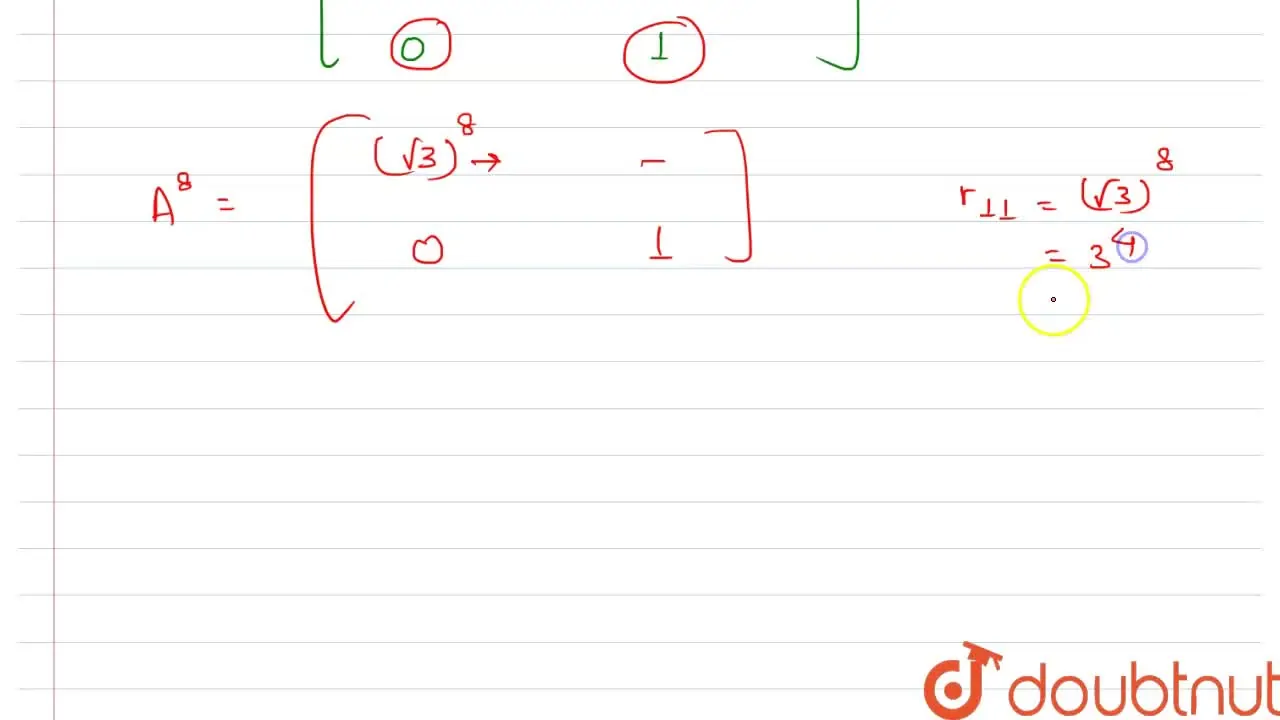
=A8PTP
=A8
Now, A2=AA=[√3−201][√3−201]
=⎡⎣(√3)2−2√3−201⎤⎦
A3=A2A=[3−2√3−201][√3−201]
=⎡⎣(√3)3−6−2√3−201⎤⎦
∴R=[rij]2×2=PTQ8P=A8=⎡⎣(√3)8−−−⎤⎦
⇒r11=81
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - ILLUSTRATION66videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - CAE 13.15videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
A square matrix P satisfies P2=I−P where I is identity matrix. If Pn=5I−8P, then n is
View SolutionLet p=⎡⎢⎣3−1−220α3−50⎤⎥⎦, where α∈R. Suppose Q=[qij] is a matrix such that PQ=kI, where k∈R,k≠0andIis the identity matrix of order 3. If q23=−k8anddet(Q)=k22, then
View SolutionLet A=[1101] and P=⎡⎢⎣cos(π6)sin(π6)−sin(π6)cos(π6)⎤⎥⎦ and Q=PAPT then PTQ2013P is:
View SolutionLet the matrices A=[√3−201] and P be any orthogonal matrix such that Q = PAP' and let R≠[r0]2−2=P'Q6Pthen
View SolutionIf P=[6−24−6]andQ=[5320] find the matrix M such that 2Q−3P−3M=0
View SolutionIf tan(pπ4)=cot(qπ4), then prove that p+q=2(2n+1),n∈Z.
View SolutionIf P is an orthogonal matrix and Q=PAPTandx=PTQ1000P then x−1 is , where A is involutary matrix. A b. I c. A1000 d. none of these
View SolutionIf P is a 3×3 matrix such that PT=2P+I, where PT is the transpose of P and I is the 3×3 identity matrix, then there exists a column matrix, X=⎡⎢⎣xyz⎤⎥⎦≠⎡⎢⎣000⎤⎥⎦ such that
View SolutionSuppose P and Q are two different matrices of order 3×n andn×p, then the order of the matrix P×Q is ?
View SolutionLet P and Q be 3×3 matrices with P≠Q . If P3=Q3andP2Q=Q2P , then determinant of (P2+Q2) is equal to (1) 2 (2) 1 (3) 0 (4) 1
View Solution