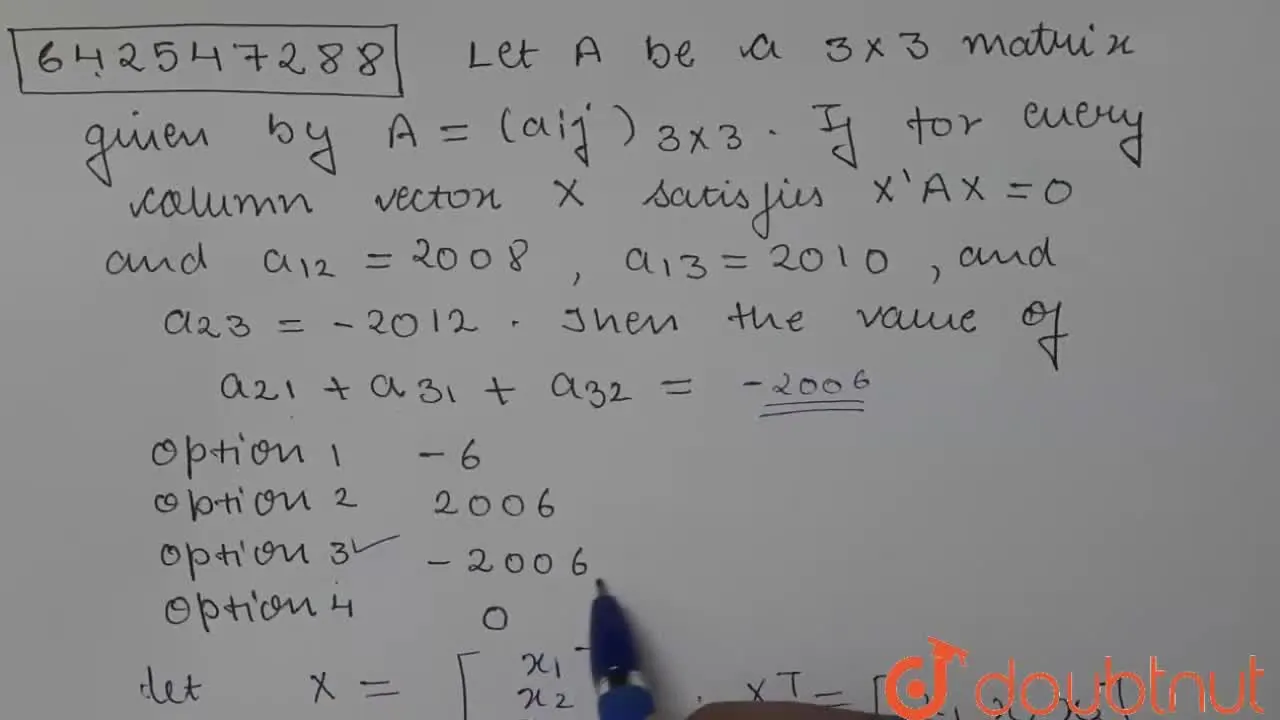Let A be a 3×3 matrix given by A=(aij)3×3. If for every column vector X satisfies X'AX=0 and a12=2008, a13=2010 and a23=−2012. Then the value of a21+a31+a32=
−6
2006
−2006
0
The correct Answer is:C
(c) Let X=⎡⎢⎣x1x2x3⎤⎥⎦
(x1x2x3)⎛⎜⎝a11a12a13a21a22a23a31a32a33⎞⎟⎠⎛⎜⎝x1x2x3⎞⎟⎠=0
a11x21+a22X22+a33x23+(a12+a21)x1x2+(a13+a31)x1x3+(a23+a32)x2x3=0
It is true for every x1, x2, x3
then a11=a22=a33=0,a12+a21=0, a13+a31=0 ,a23+a32=0
∴A is a skew symmetric matrix
a21=−2008
a31=−2010
a32=2012
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - JEE Advanced (Single Correct Answer Type)5videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
Let A be a 3×3 matrix given by A=[aij]. If for every
column vector X,XTAX=Oanda23=−1008, the sum
of the digits of a32 isView SolutionThe square matrix A=[aij given by aij=(i−j)3, is a
View SolutionConsider A=[a11a12a21a22] and B=[1121] such that AB=BA. then the value of a12a21+a11a22 is
View SolutionIf α and β are roots of the equation x2−3x+1=0 and an=αn+βn−1 then find the value of a5−a1a3−a1
View SolutionLet A be the 2×2 matrix given by A=[aij] where aij∈{0,1,2,3,4} such theta a11+a12+a21+a22=4 then which of the following statement(s) is/are true ?
View SolutionConstruct a matrix [aij]3×3 , where aij=2i−3j.
View SolutionA1 and A2 are two vectors such that |A1|=3,|A2|=5 and |A1+A2|=5 the value of (2A1+3A2).(2A1−2A2) is
View SolutionIf Aij is the cofactor of the element aij of the determinant ∣∣ ∣∣2−3560415−7∣∣ ∣∣, then write the value of a32.,A32.
View SolutionIf A is a 3×3 matrix, whose elements are given by aij=13|−3i+j|, then write the value of a23 .
View SolutionIf (1+x+x2)25=a0+a1x+a2x2+……………..a50x50
then the value of
a0+a2+a4+…………+a50 isView Solution