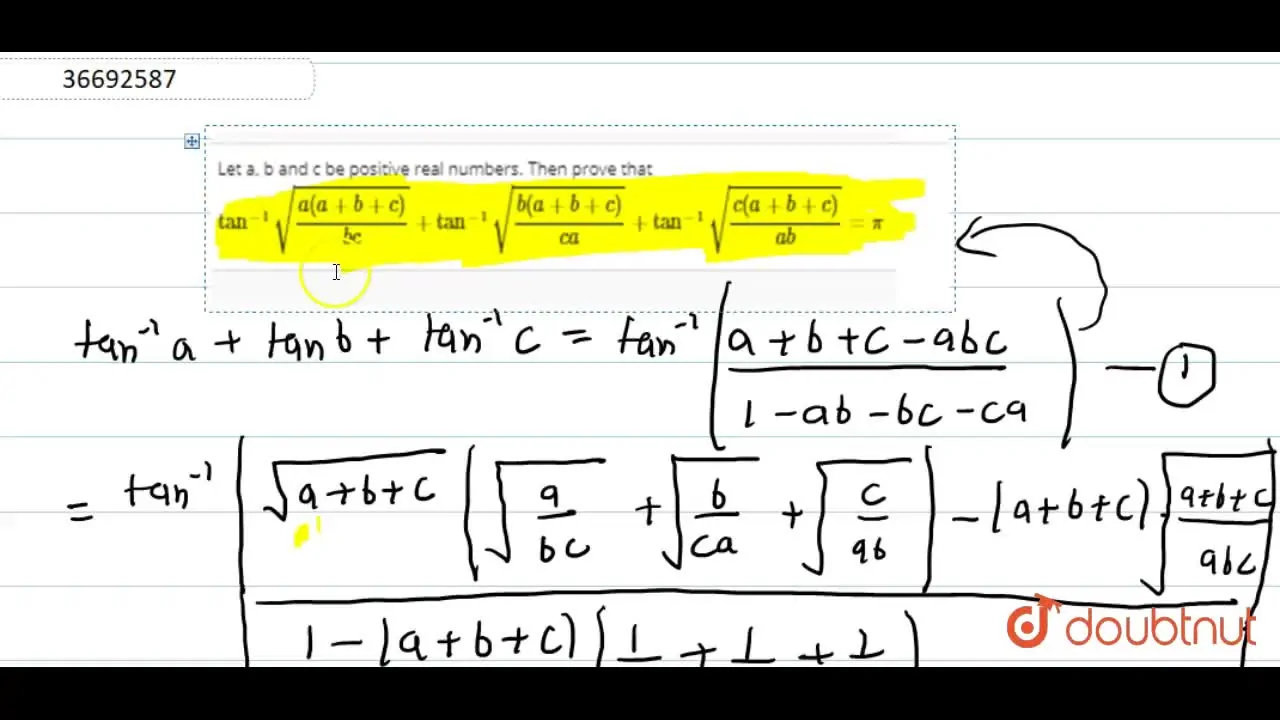
Let a, b and c be positive real numbers. Then prove that tan−1√a(a+b+c)bc+tan−1√b(a+b+c)ca+tan−1√c(a+b+c)ab=π
Let
S=tan−1√a(a+b+c)bctan−1√b(a+b+c)ca+tan−1√c(a+b+c)ab
Now, √a(a+b+c)bc√b(a+b+c)ca=a+b+cc=1+bc+ac>1
S=π+tan−1.√a(a+b+c)bc+√b(a+b+c)ca1−√a(a+b+c)bc√b(a+b+c)ca+tan−1√c(a+b+c)ab
=π+tan−1.√a+b+cc(√ab+√ba)1−a+b+cc+tan−1√c(a+b+c)ab
=π+tan−1⎛⎝−√c(a+b+c)ab⎞⎠+tan−1√c(a+b+c)ab
=π
Related Playlists
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.112videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.26videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year20videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
tan−1√a(a+b+c)bc+tan−1√b(a+b+c)ca+tan−1√c(a+b+c)ab is equal to
View SolutionIf a,b,c be positive real numbers and the value of θ=tan−1√a(a+b+c)bc+tan−1√b(a+b+c)ca+tan−1√c(a+b+a)(ab) then tanθ is equal to
View SolutionIf a,b,c>0 and θ=tan−1√a(a+b+c)bc+tan−1√b(a=b+c)ca+tan−1√c(a+b+c)ab,
Then 3π/2π=View SolutionIf a,b,c>0 and s=a+b+c2,provethat tan−1√2asbc+tan−1√2bsca+tan−1√2csab=π
View SolutionIf a,b,c are real positive numbers and θ=tan−1[a(a+b+c)bc]12+tan−1[b(a+b+c)ca]12+tan−1[c(a+b+c)ab]12, then tanθ equals
View SolutionIf a, b, c are positive real numbers, then √a−1b × √b−1 c × √c−1a is equal to: (a) 1 (b) abc (c) √abc (d) 1abc
View SolutionIf in △ABC,C=90∘ then prove that tan−1(ac+b)+tan−1(ba+c)=π4.
View SolutionIf a, b and c are distinct positive real numbers and a2+b2+c2=1, then ab + bc + ca is
View Solutionयदि a, b, c धनात्मक वास्तविक संख्याएँ हैं, तो √a−1b×√b−1c×√c−1a का मान होगाः
View SolutionIf a,b,c are positive real numbers and a≥b≥c. Then,aba+b+bcb+c+cac+a
View Solution