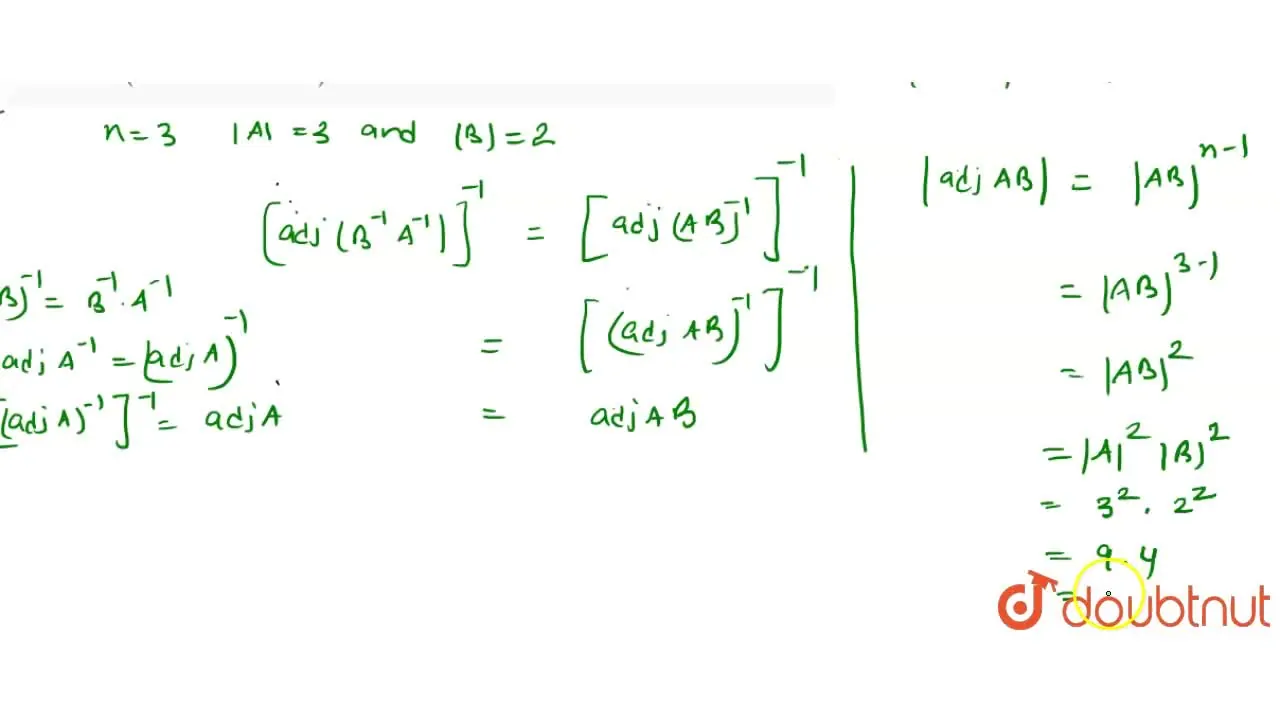Let A and B are two square matrices of order 3 such that det. (A)=3 and det. (B)=2, then the value of det. ((adj. (B−1A−1))−1) is equal to _______ .
The correct Answer is:36
(adj. (B−1A−1))−1=(adj. (AB)−1)−1
=((adj. (AB))−1)−1 [as adj. A−1=(adj. A)−1]
= adj. (AB)
∴|(adj. (AB))|=|AB|2=|A|2|B|2=9×4=36
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Archives (Single correct Answer type)11videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - JEE Advanced (Single Correct Answer Type)5videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Matrix Type5videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
Let A be a square matrix of order 3 such that det. (A)=13, then the value of det. (adj. A−1) is
View SolutionIf A and B are square matrices of order 3 such that |A|=−1 , |B|=3 , then find the value of |3AB| .
View SolutionIf A and B are square matrices of order 3 such that |A|=–1,|B|=3, then find the value of |2AB|.
View SolutionIf A and B are square matrices of order 3 such that |A|=3and|B|=2, then the value of ∣∣A−1adj(B−1)adj(3A−1)∣∣ is equal to
View SolutionLet A and B be two square matrices of order 3 such that |A|=3and|B|=2, then the value of
∣∣A−1.adj(B−1).adj(2A−1)∣∣ is equal to (where adj(M) represents the adjoint matrix of M)View SolutionIf A and B are square matrices of order 3 such that AAT=3B and 2AB−1=3A−1B, then the value of |B|216 is equal to
View SolutionIf A and B are squar matrices of order 3 such that |A|=-1, |B|=3 then |3AB| is equal to
View SolutionLet A and B be two invertible matrices of order 3×3. If det. (ABAT) = 8 and det. (AB−1) = 8, then det. (BA−1BT) is equal to
View SolutionIf A, B and C are three sqare matrices of the same order such that A = B + C, then det A is equal to
View SolutionLet A and B are two non - singular matrices of order 3 such that |A|=3andA−1B2+2AB=O, then the value of ∣∣A4−2A2B∣∣ is equal to (where O is the null matrix of order 3)
View Solution