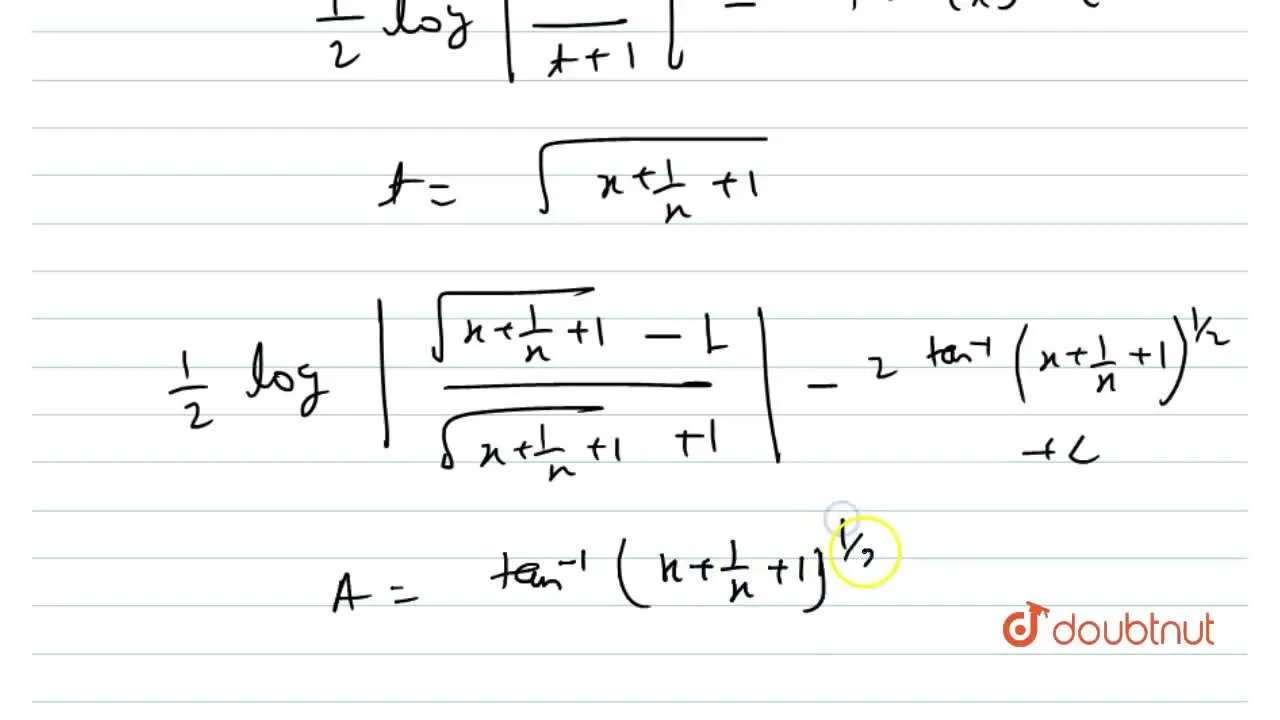∫x(x−1)(x2+1)(x+1)√x3+x2+x=12log∣∣
∣
∣∣√x+1x+1−1√x+1x+1+1∣∣
∣
∣∣−A+c.
Then the value of A is equal to
A
cos−1√1+1x
B
tan−1√x+1x+1
C
cot−1√x+1x
D
sin−1√x+1x+1
Video Solution
Text Solution
The correct Answer is:B
We have ∫x(x−1)(x2+)(x+1)√x3+x2+xdx
=∫x(x2−1)(x2+1)(x+1)2√x3+x2+xdx
=∫x3(1−1x2)x3(x+1x)(√x+1√x)2√x+1x+1dx
=∫(1−1x2)(x+1x)(x+1x+2)√x+1x+1dx
I=∫2t(t2−1)(t2+1)√t2dt
where x+1x+1=t2
=∫2(t2−1)(t2+1)dt
=∫1t2−1dt−∫1t2+1dt
=12log∣∣∣t−1t+1∣∣∣−tan−1t+c
=12log∣∣
∣
∣∣√x+1x+1−1√x+1x+1+1∣∣
∣
∣∣−tan−1√x+1x+1+c
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Subjective Type6videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Comprehension Type2videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - JEE Advanced Previous Year1videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year14videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
Similar Questions
If ∫x(x−1)(x2+1)(x+1)√x3+x2+xdx
=12loge∣∣ ∣∣√f(x)−1√f(x)+1∣∣ ∣∣−tan−1√f(x)+C, then ,the value of f(1) isView SolutionIf ∫x+1(x2+x+1)dx√x2+x+1=Kx−1√x2+x+1+C then the value of K is
View Solution∫1−1(√1+x+x2−√1−x+x2)dx=
View Solution∫21x−1x+1.1√x3+x2+xdx
View SolutionIf I=∫xcosx+1√2x3esinx+x2dx=A9log∣∣∣√2xesinx+1−1√2xesinx+1+1∣∣∣+C, then A is equal to
View SolutionIf ∫dxx3(x−1)1/2=√x−1(3x+2)4x2+Ktan−1√x+1+C then the value of K is
View Solution∫[1+1(1+x2)−2√1−x2+5x√x2−1+ax]dx
View Solution∫[1+1(1+x2)−2√1−x2+5x√x2−1+ax]dx
View Solution∫(x+1)√1−x−x2dx=−13(1−x−x2)32+A+c .Then the value of A is
View Solution∫1−1(√1+x+x2−√1−x+x2)dx=
View Solution