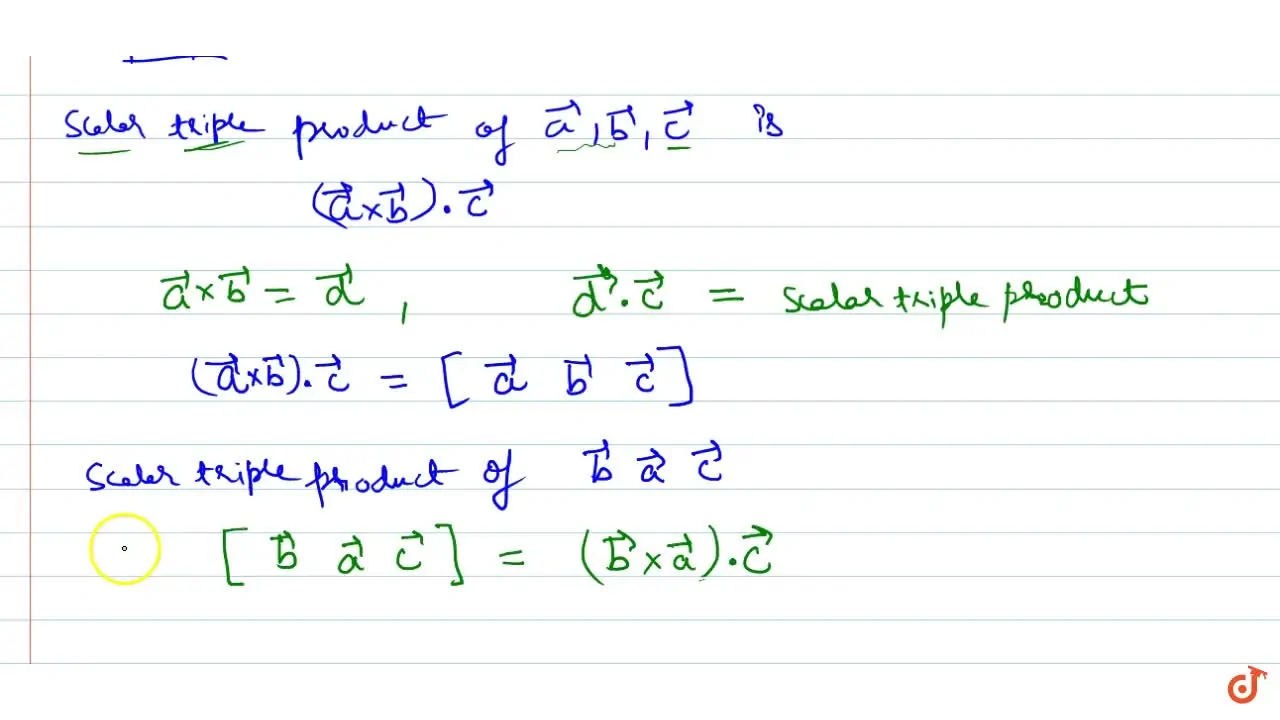Introduction and definition of Scalar triple product
Step by step video & image solution for Introduction and definition of Scalar triple product by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Scalar Triple Product |
View SolutionVector triple product
View SolutionIntroduction and Definition of Irrational numbers.
View SolutionVector Triple Product
View SolutionImage OF point in plane OF tetrahedron || Scalar triple product
View SolutionScalar Triple Product , Properties OF Scalar triple product || General expression OF Triple product & illustration
View Solution→a.(→b×→c) is called the scalar triple product of →a,→b,→c and is denoted by [→a→b→c].If→a,→b,→c are cyclically permuted the vaslue of the scalar triple product remasin the same. In a scalar triple product, interchange of two vectors changes the sign of scalar triple product but not the magnitude. in scalar triple product the the position of the dot and cross can be interchanged privided the cyclic order of vectors is preserved. Also the scaslar triple product is ZERO if any two vectors are equal or parallel. If →a,→b,→c are coplanar then [→b+→c→c+→a→a+→b=] (A) 1 (B) -1 (C) 0 (D) none of these
View Solution→a.(→b×→c) is called the scalar triple product of →a,→b,→c and is denoted by [→a→b→c].If→a,→b,→c are cyclically permuted the vaslue of the scalar triple product remasin the same. In a scalar triple product, interchange of two vectors changes the sign of scalar triple product but not the magnitude. in scalar triple product the the position of the dot and cross can be interchanged privided the cyclic order of vectors is preserved. Also the scaslar triple product is ZERO if any two vectors are equal or parallel. [→a+→b→b+→c→c+→a] is equal to (A) 2[→a→b→c] (B) 3[→a,→b,→c] (C) [→a,→b,→c] (D) 0
View Solution→a.(→b×→c) is called the scalar triple product of →a,→b,→c and is denoted by [→a→b→c].If→a,→b,→c are cyclically permuted the vaslue of the scalar triple product remasin the same. In a scalar triple product, interchange of two vectors changes the sign of scalar triple product but not the magnitude. in scalar triple product the the position of the dot and cross can be interchanged privided the cyclic order of vectors is preserved. Also the scaslar triple product is ZERO if any two vectors are equal or parallel. (A) [vecb-vecc vecc-veca veca-vecb](B)[veca vecb vecc] (C) 0 (D) none of these
View SolutionIllustration Based on Triangle|| Illustration Based on Tetrahedron|| Scalar Triple Product
View Solution