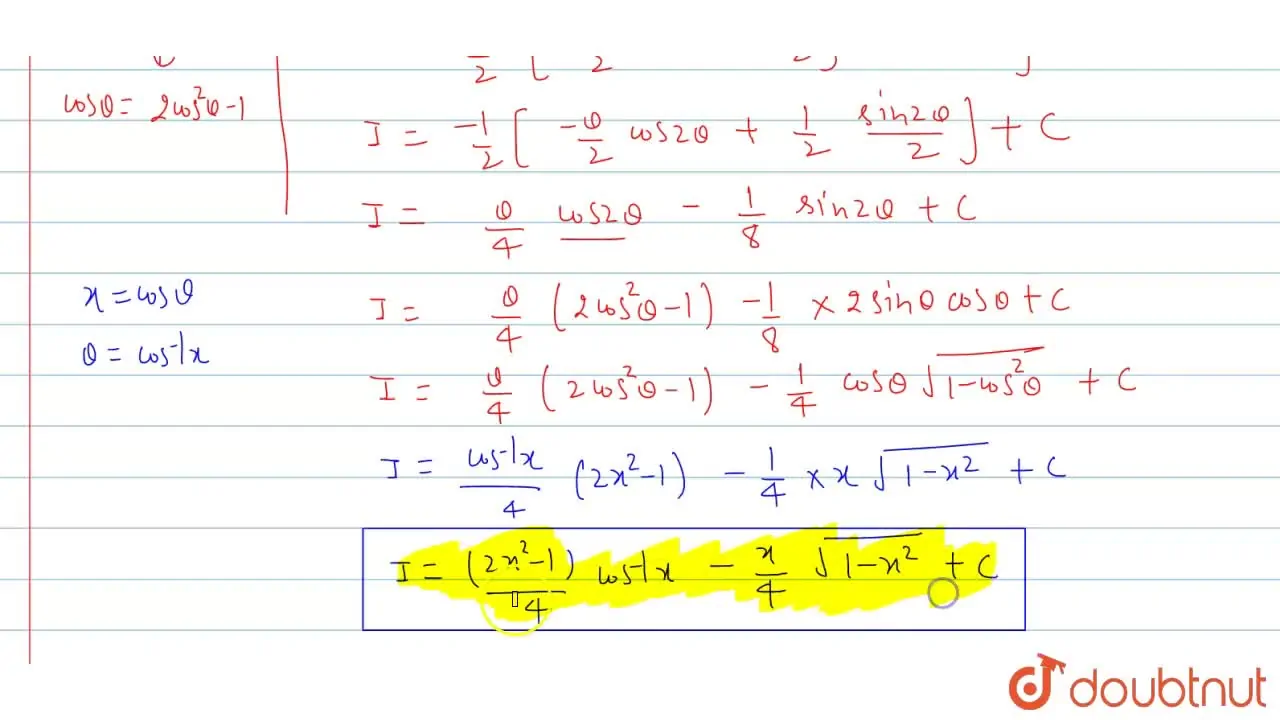Integrate the function xcos−1x
Video Solution
Text Solution
Let I=∫xcos−1xdx
Applying integration by parts, by taking cos−1x as first function and x as second function
I=cos−1x∫xdx−∫{(ddx(cos−1x))}∫(xdx)dx
=cos−1⋅x(x22)−12∫1−x2−1√1−x2⋅dx
=cos−1⋅x(x22)−12∫{√1−x2+−1√1−x2}dx
=cos−1⋅x(x22)−12∫{√1−x2+12⋅∫−1√1−x2}dx
=cos−1⋅x(x22)−12I1−12cos−1x.......(1)
where, I1=∫√1−x2dx
Applying integration by parts
⇒I1=√1−x2∫1dx−∫ddx√1−x2∫1dx
⇒I1=x√1−x2−∫−x2√1−x2⋅dx
⇒I1=x√1−x2−∫1−x2−1√1−x2⋅dx
⇒I1=x√1−x2−{∫√1−x2dx+∫−1√1−x2⋅dx}
⇒I1=x√1−x2−{I1+cos−1x}
⇒2I1=x√1−x2−cos−1x<br>I1=x√1−x22−12⋅cos−1x
Substituting in (1), we obtain
I=[(2x2−1)4]cos−1x−x4x⋅√1−x2+c+C
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.1010videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.714videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.922videos
INTEGRALS
- BOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.112videos
DIFFERENTIAL EQUATIONS
- BOOK - NCERTCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE17videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Integrate the function xcos−1x
View SolutionIntegrate the function xcos−1x√1−x2
View SolutionIntegrate the function xsin−1x
View SolutionIntegrate the function xtan−1x
View SolutionIntegrate the function (sin−1x)2
View SolutionIntegrate the function(x3−1)(x4+1)(x+1)
View SolutionIntegrate the function sin−1(2x1+x2)
View SolutionIntegrate the functions(x3−1)13x5
View SolutionIntegrate the function xlogx
View SolutionIntegrate the function (x2+1)logx
View Solution