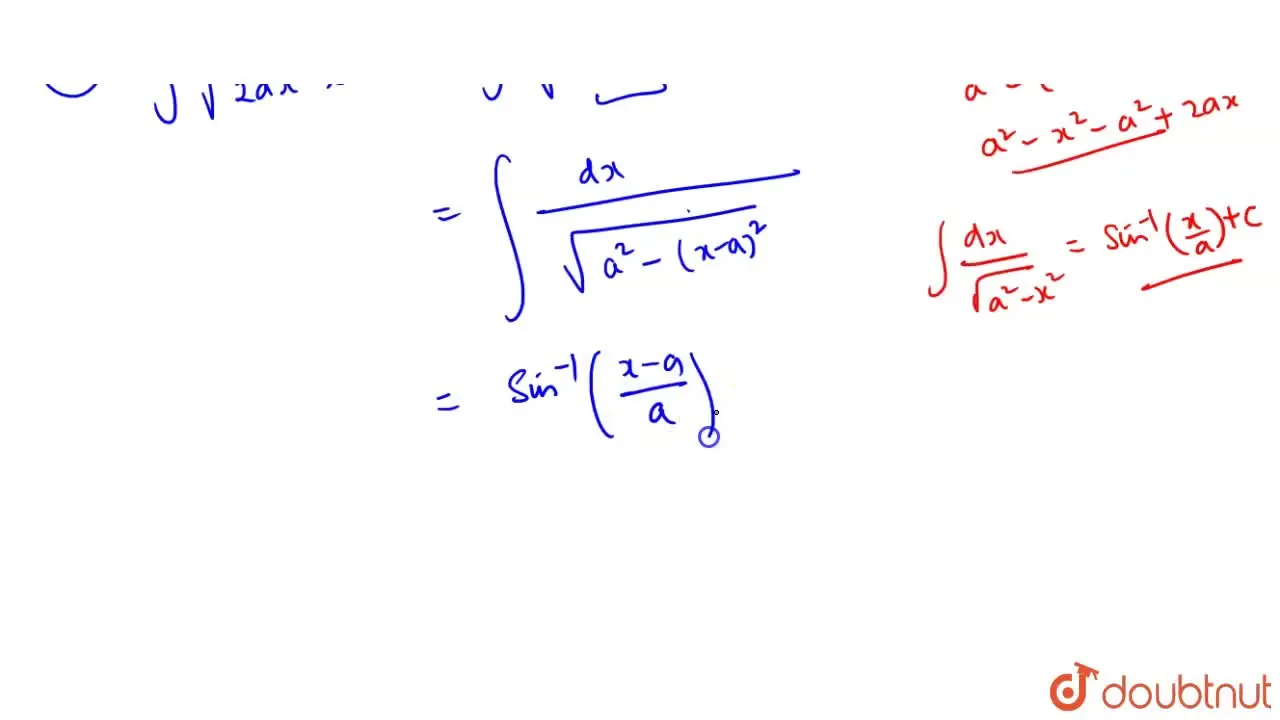Integrate the following integrals
Video Solution
Text Solution
put
put
|
Updated on:21/07/2023
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - INTEGRALSEXERCISE - Competition level Questions76videos
INTEGRALS
- BOOK - AAKASH INSTITUTECHAPTER - INTEGRALSEXERCISE - Objective Type Questions (Only one answer)64videos
INTEGRALS
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment Section - J (Aakash Challengers Questions)4videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - J)(ANKASH CHALLENGERS QUESTIONS)4videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
(i) ∫dxx√x2−1 (ii) ∫dxx√ax−x2
View Solution(i) ∫dx√x(1−2x)
(ii) ∫dx√2x−x2View SolutionIntegrate the following integral, I=∫4x+1x2+3x+2dx
View SolutionIntegrate the Following Integral ∫2x−3√2x2−6x+1dx
View SolutionIntegrate the Following Integral ∫2x+3√x2+2x+10dx
View SolutionEvaluate the following integration
∫dx√x+1−√xView SolutionEvaluate the following integrals:
∫√5−2x−x2dxView SolutionEvaluate the following integrals:
∫x√x+2dxView SolutionEvaluate the following integrals :
(i)∫1(x+1)√2x−3dx
(ii)∫1(x+1)√x2+x−1dx
(iii)∫1(x2+3x+3)√x+1dx
(iv)∫1(x2−3x+2)√x2−2dxView SolutionEvaluate the following integrals.
∫2x−3√2x−1dxView Solution