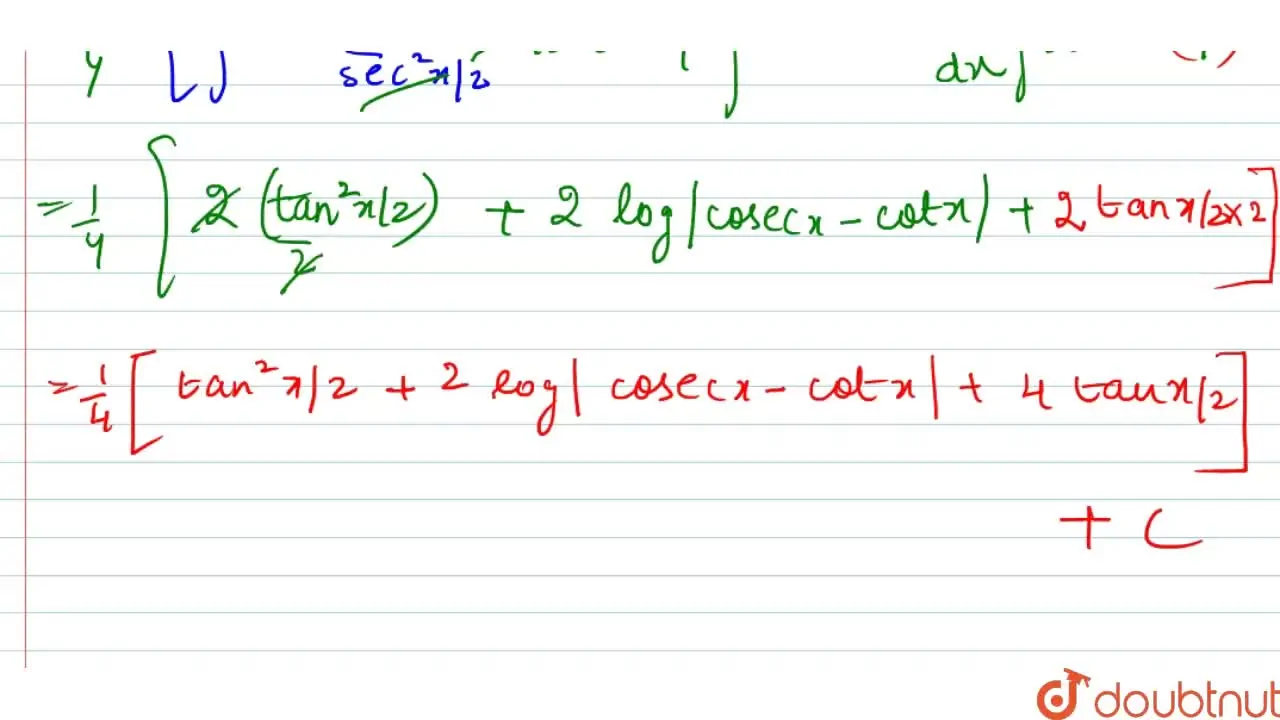∫1+sinxsinx(1+cosx)dx
Video Solution
|
Answer
Step by step video & image solution for int(1+sinx)/(sinx(1+cosx))dx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
Similar Questions
Evaluate: ∫sinxsinx−cosxdx
View SolutionEvaluate: ∫sinx+cosxsinx−cosxdx
View SolutionEvaluate the following integral: ∫π0sinxsinx+cosxdx
View SolutionEvaluate: ∫1+sinx√x−cosxdx
View SolutionEvaluate: ∫1+sinx√x−cosxdx
View Solution∫x−sinx1−cosxdx
View Solution∫x−sinx1−cosxdx
View SolutionEvaluate: ∫sinx+2cosx2sinx+cosxdx
View SolutionIf ∫sinx+3cosxsinx+cosxdx=kx2+ln(sinx+cosx), then k is_________.
View SolutionEvaluate: ∫ex(1−sinx1−cosx)dx
View Solution