In the quadrilateral ABCD,AC=8√3cm, angle CAB=30∘ angle ADC=60∘ angle ABC = angle ACD=90∘. Find the area of the quadrilateral ABCD.
Video Solution
|
Answer
Step by step video & image solution for In the quadrilateral ABCD, AC = 8sqrt3 cm, angle CAB = 30^@ angle ADC = 60^@ angle ABC = angle ACD = 90^@. Find the area of the quadrilateral ABCD. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In the quadrilateral ABCD shown below, ∠DAB=∠DCX=120∘. If ∠ABC=105∘, then what is the value of ∠ADC?
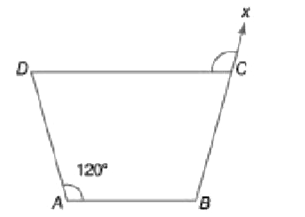 A45∘B60∘C75∘D95∘
A45∘B60∘C75∘D95∘ - Question 2 - Select One
In cyclic quadrilateral ABCD,∠CAB=30∘ and ∠ABC=100∘ Then,∠ADB=
A50∘B100∘C75∘D60∘ - Question 3 - Select One
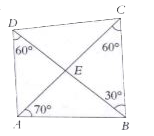
In the given figure ABCD is a quadrilateral ∠ADB=60∘,∠BAC=70∘,∠DBC=30∘,and∠ACB=60∘. Find ∠DACA30∘B40∘C50∘D60∘
In cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCDView SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCAView SolutionIn cyclic quadrilateral ABCD , AD = BC, ∠BAC=30∘and∠CBD=70∘ , find : angle ADC .
View SolutionIn a cyclic quadrilateral ABCD ∠A:∠C=3:1and angle B : angle D = 1 : 5 find each angle of the quadrilateral
View SolutionConstruct a quadrilateral ABCD in which AB = 4.5 cm , BC = 3.8 cm ∠BCD=90∘∠BAD=60∘and∠ABC=120∘
View Solution
