In the given figure if and BD is perpendicular to AC then
prove that:
(iii)
(v)
(vii)

(i) In
( just proved)
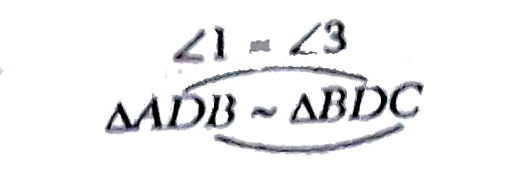 (AA corollary) Hence proved.
(AA corollary) Hence proved.
(ii)
( common)
 (AA corollary) Hence poved.
(AA corollary) Hence poved.
(iii) In
(common)
 [from part (i)
[from part (i)
(corresponding sides of similar triangles are proportional)
(iv) For . we need to prove two similar which contain BD, AD and DC as sides.
Obviosly these are , we have proved these as similar in part (i). so ,
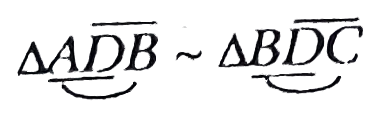 [from part (ii)]
[from part (ii)]
( corresponding sides of similar triangle are proportional)
Hence proved.
(v) For we need to prove two triangles similar which contain AB, AD and AC as sides. Obviosusly these are . we have already proved these as similar in part (ii)
[ from part (ii) ]
.... (1) Hence proved
(vi) For we need to prove two triangles similar which contains BC, CD and AC as sides. Obviosly these are , we have proved these triangles as similar in part (iii)
so,
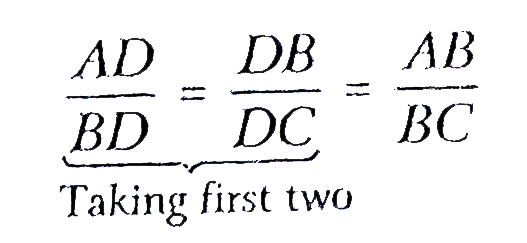 ( cossesponding sides of similar triangle are proportional)
( cossesponding sides of similar triangle are proportional)
....(2) Hence proved.
(vii) Addings results (1) and (2), we get
Hence proved.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a23videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
In the adjoining figure ∠ABC=90∘ and BD is perpendicular to AC express (AD×DC) in terms of BD
View SolutionIn the given figure if AC=BD then prove that AB=CD
 View Solution
View SolutionIn the given figure ∠ABC=90∘andCD⊥AB. Prove that BC2AC2=BDAD
 View Solution
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
 View Solution
View SolutionIn the given figure AD=BC,AC=BD. Then ΔPAB is
 View Solution
View SolutionIn a triangle ABC, ∠B=90∘,AB=8cm,BC=6cm. BD is perpendicular to AC, then find the length of CD, AD and BD.
View SolutionIn the given figure, if AC = BD, then prove that AB = CD.
 View Solution
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2View SolutionIn ΔABC,∠C=90∘ and CD is perpendicular to AB at D. If ADBD=√k, then ACBC=?
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
diagonal AC = diagonal BD
 View Solution
View Solution


