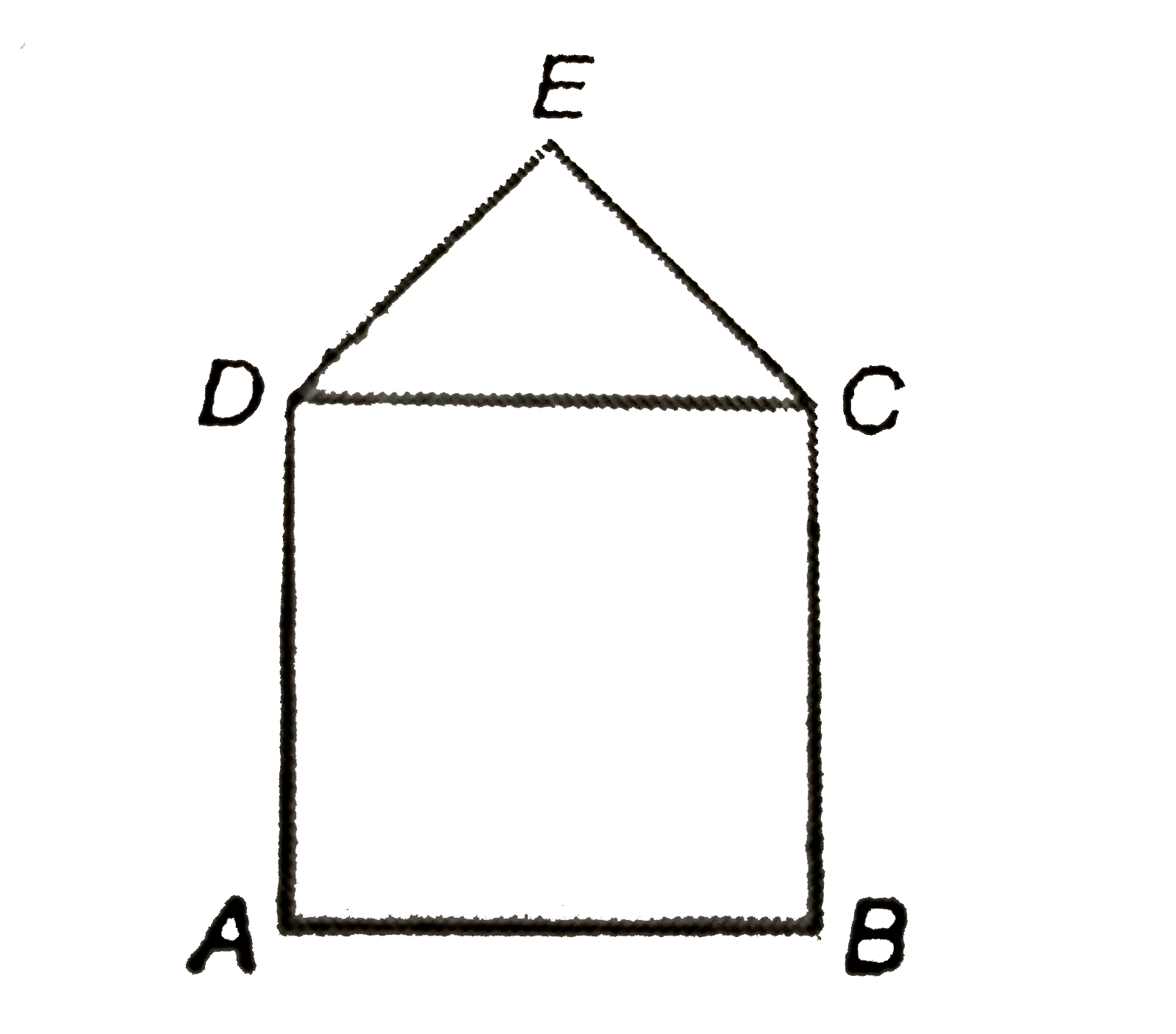
In the given figure, ABCD is a square and ΔBCT is an equilateral triangle. Find ∠BTD.
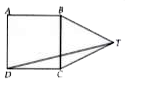
30∘
15∘
45∘
35∘
Step by step video & image solution for In the given figure, ABCD is a square and DeltaBCT is an equilateral triangle. Find /_BTD. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBook:MTG IIT JEE FOUNDATIONChapter:UNDERSTANDING QUADRILATERALSExercise:EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 MATCH THE FOLLOWING)
Explore 1 Video
- UNDERSTANDING QUADRILATERALSBook:MTG IIT JEE FOUNDATIONChapter:UNDERSTANDING QUADRILATERALSExercise:EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 ASSERTION AND REASON TYPE)
Explore 5 Videos
- UNDERSTANDING QUADRILATERALSBook:MTG IIT JEE FOUNDATIONChapter:UNDERSTANDING QUADRILATERALSExercise:EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-1)
Explore 35 Videos
- SQUARES AND SQUARE ROOTSBook:MTG IIT JEE FOUNDATIONChapter:SQUARES AND SQUARE ROOTSExercise:Olympiad/HOTS Corner
Explore 20 Videos
- VISUALISING SOLID SHAPESBook:MTG IIT JEE FOUNDATIONChapter:VISUALISING SOLID SHAPESExercise:OLYMPIAD/HOTS CORNER
Explore 10 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD is a square. Find x.
 A60∘B120∘C100∘D110∘
A60∘B120∘C100∘D110∘In the given diagram, ABCD is a square and Δ BCT is an equilateral triangle. ∠ BTD equals
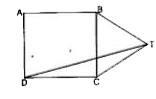 A30∘B15∘C45∘D35∘
A30∘B15∘C45∘D35∘In the given figure, PQRS is a square and SRT is an equliateral triangle. What is the value (in digrees) of ∠SOR ?
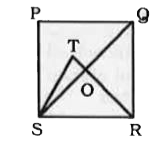 A45B55C60D75
A45B55C60D75
In the given figure ABCD is a square with side 15 and BCE is an equilateral triangle. The ratio of the shaded region to the unshaded region is :
View SolutionIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
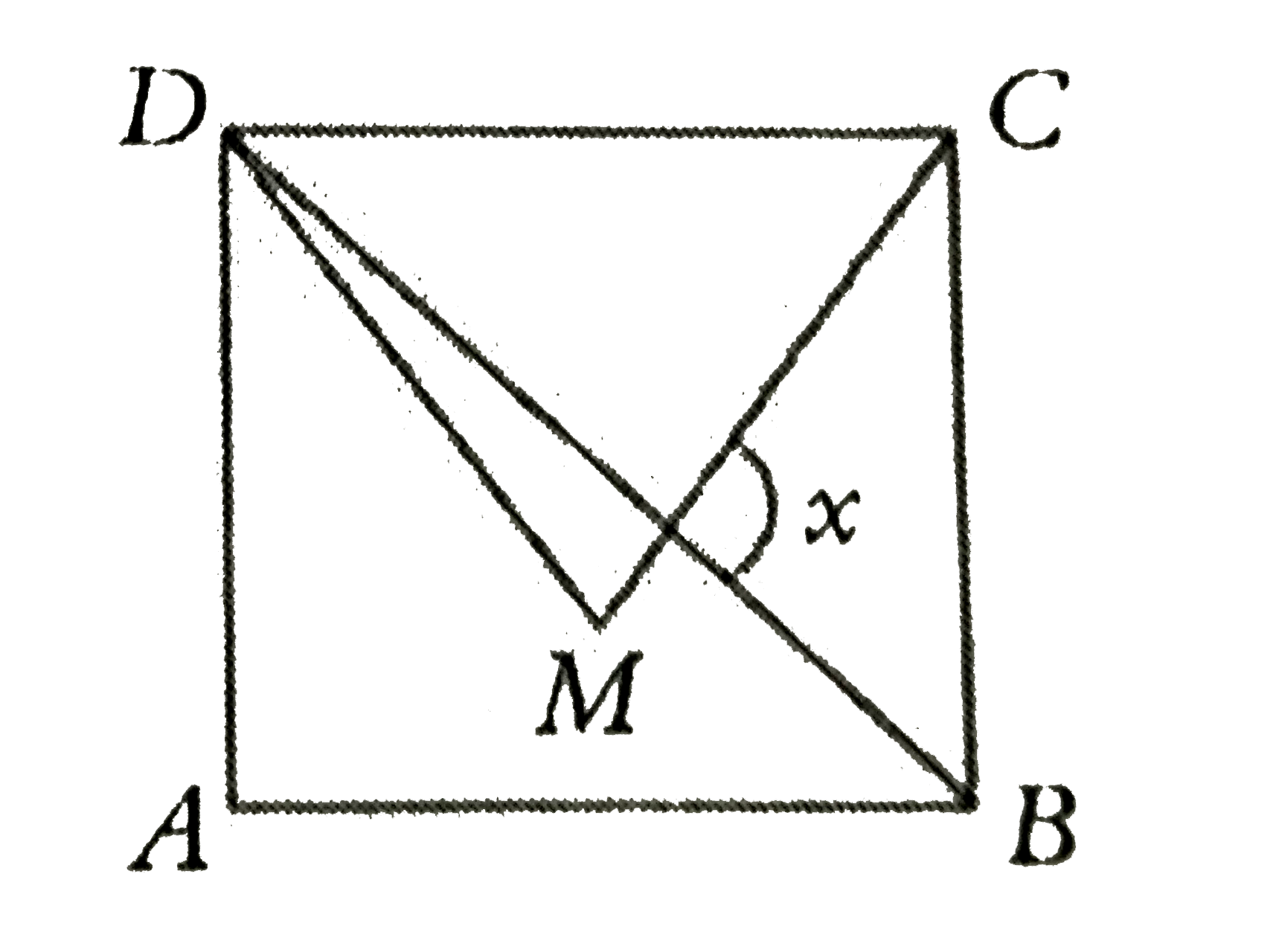
View SolutionFind the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

View SolutionIn the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
View SolutionABCD is a square and ABE is an equilateral triangle outside the square then
View Solution