In the given figue, ⇒∠BAD=65∘∠ABD=70∘,∠BDC=45∘.
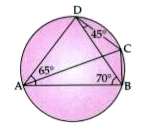
(ii) Find ∠ACB
Step by step video & image solution for In the given figue, rArrangleBAD=65^(@) angleABD=70^(@), angleBDC=45^(@). (ii) Find angleACB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
In the given figue, ⇒∠BAD=65∘∠ABD=70∘,∠=45∘.
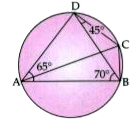
(i) Prove that AC is a diameter of the circle.View SolutionIn the given figure ∠BAD=60∘,∠ABD=70∘∠BDC=45∘
(i) prove that AC is a diameter of the circle
(ii) Find ∠ACB
(##SEL_RKB_ICSE_MAT_X_C17_E02_002_Q01.png" width="80%">View SolutionIn the given figure, find (i)∠XOD(ii)∠XOC
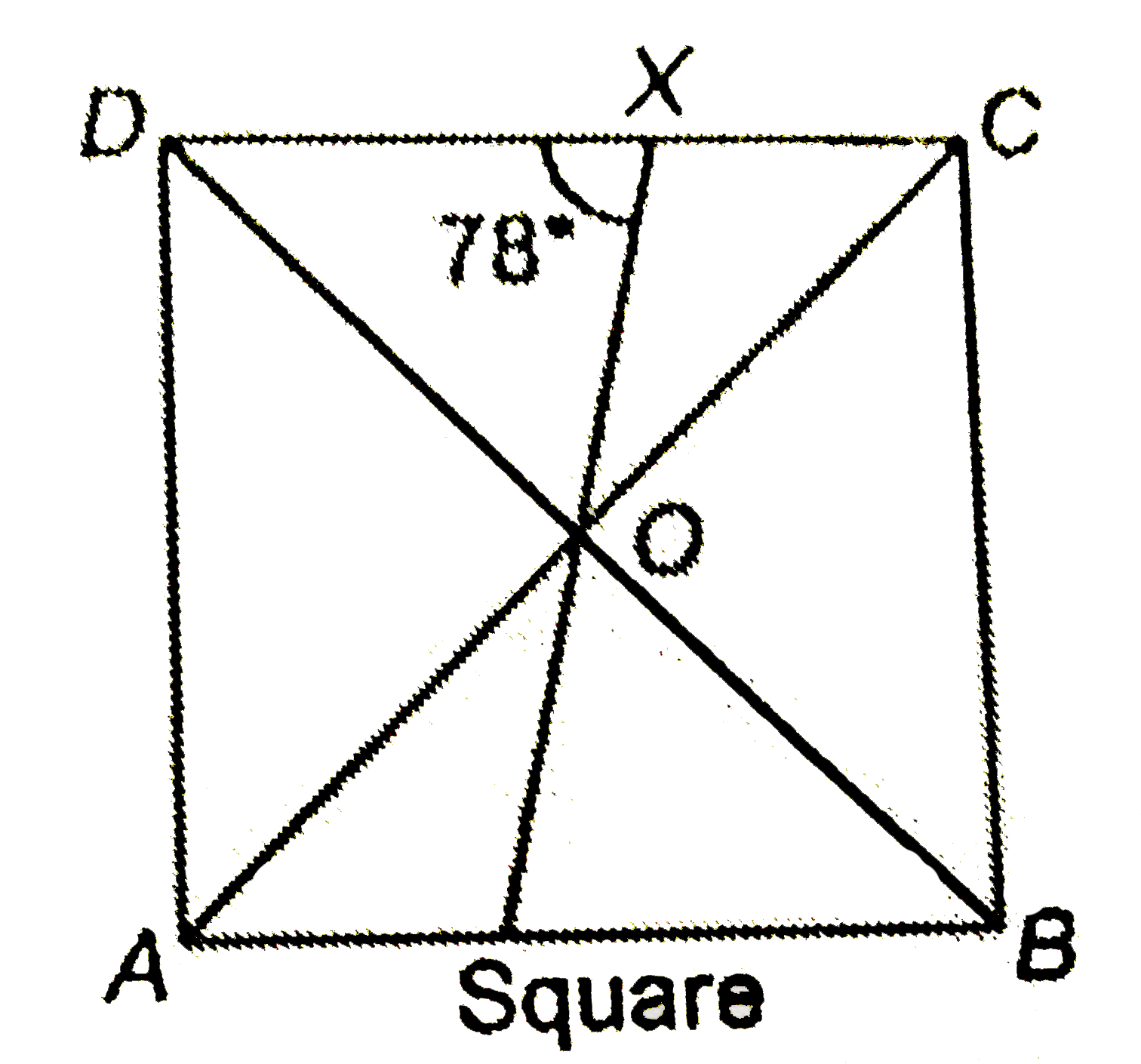 View Solution
View SolutionIn the given figure AB=DB,AC=DC if ∠ABD=58∘,∠DBC=2x−4∘,∠ACB=y+15∘ and ∠DCB=63∘, find the values of x and y.
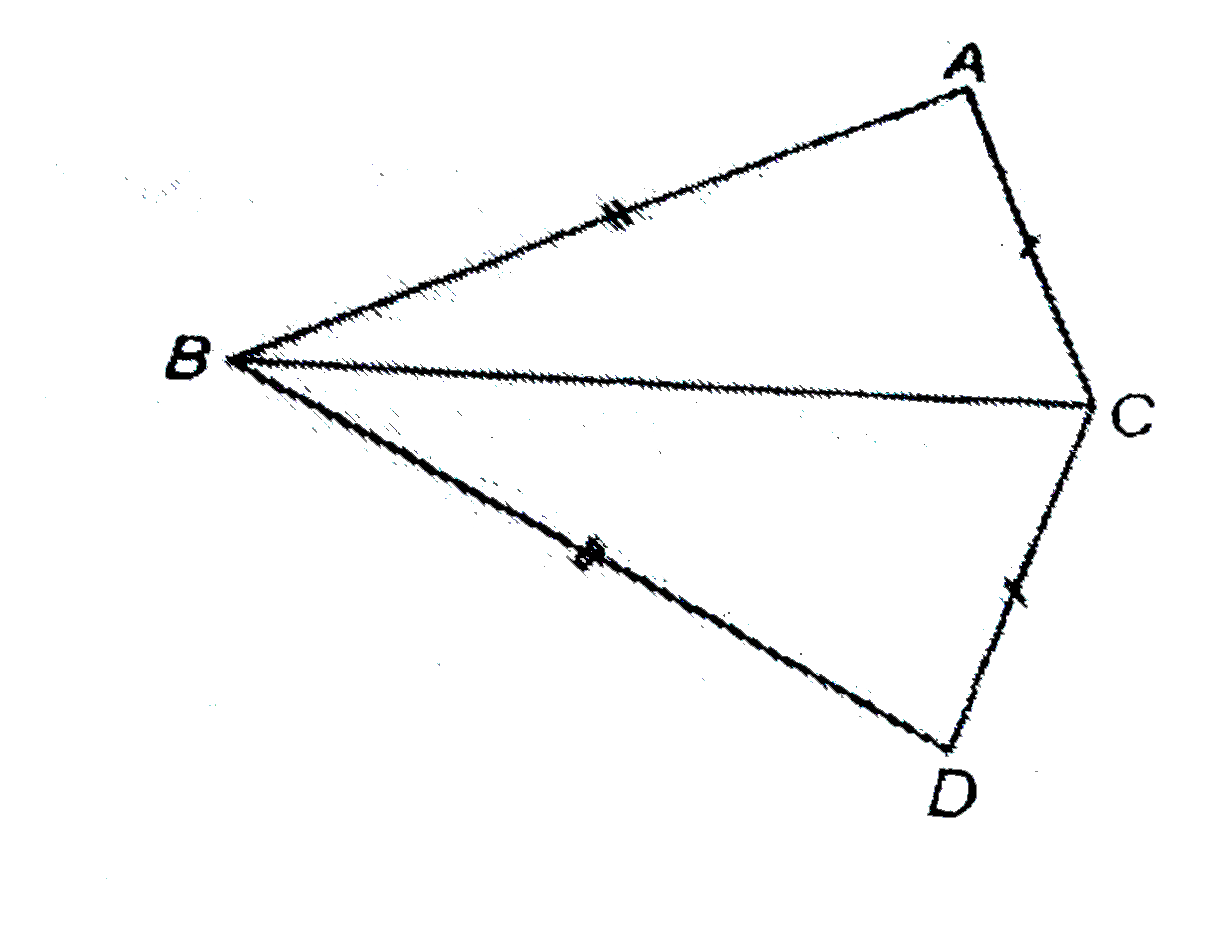 View Solution
View SolutionIn the given figure if find, ∠AOC=45∘, find ∠BOD
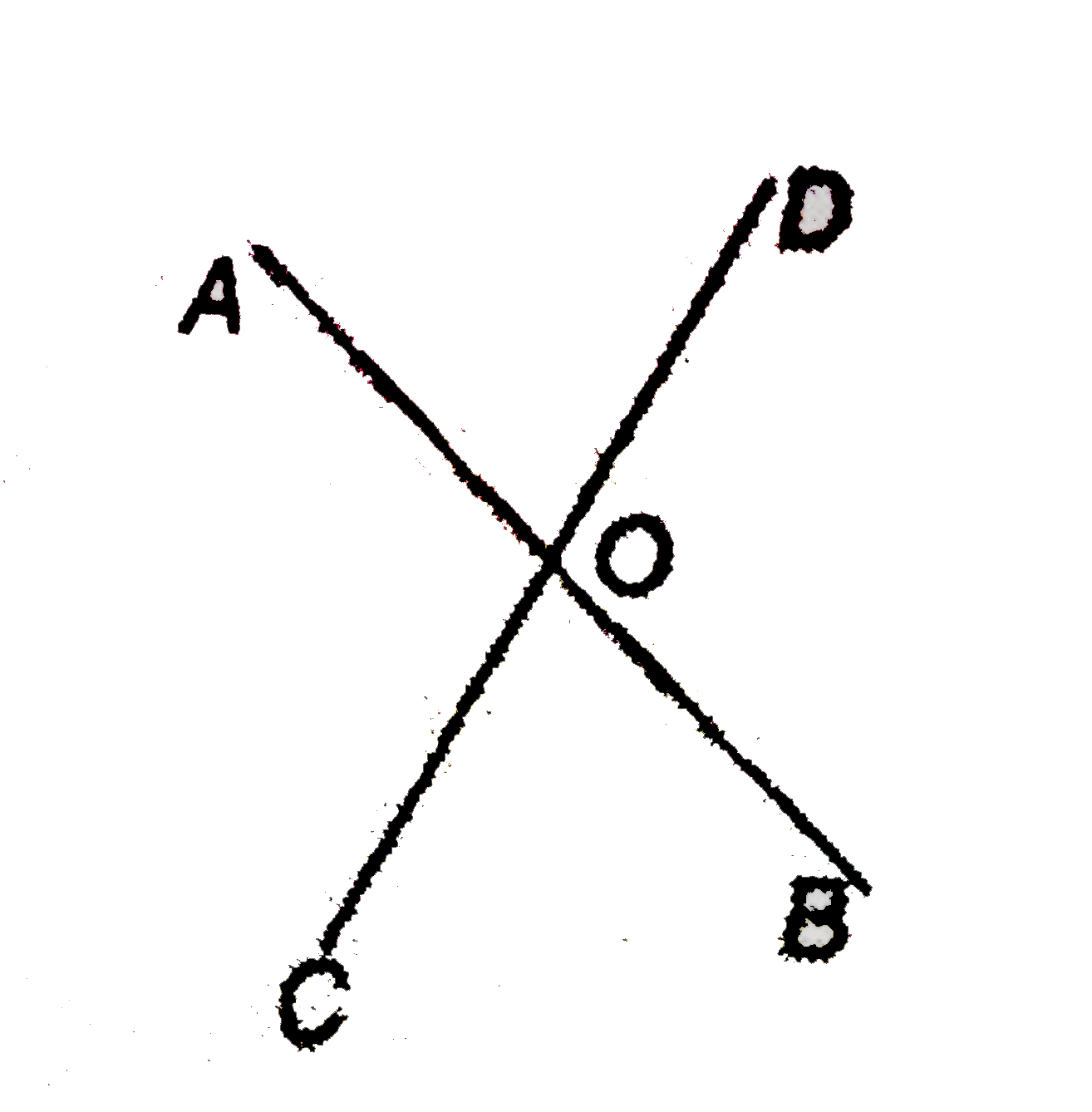 View Solution
View SolutionIn the given figure, find ∠ADB, if ∠DCB=100∘ and ∠DBA=70∘.
 View Solution
View SolutionIn the given figure, AB = DB and AC = DC. If ∠ABD=58∘,∠DBC=(2x−4)∘,∠ACB=y+15∘ and ∠DCB=63∘, Find the value of x and y.
 View Solution
View SolutionIn the following figure , AB = AC , EC = ED ∠ABF=45∘and∠ABC=70∘
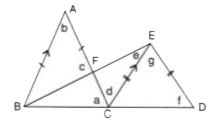
Find the angles represented by letters a,b,c,d,e,f and g.View SolutionIn the given figure, line m is parallel to n. Given that
∠BAP=3x+10∘,∠BAC=3x
∠ABC=3y−5∘,∠ACB=x+y+5∘
Find the valuses of x and y
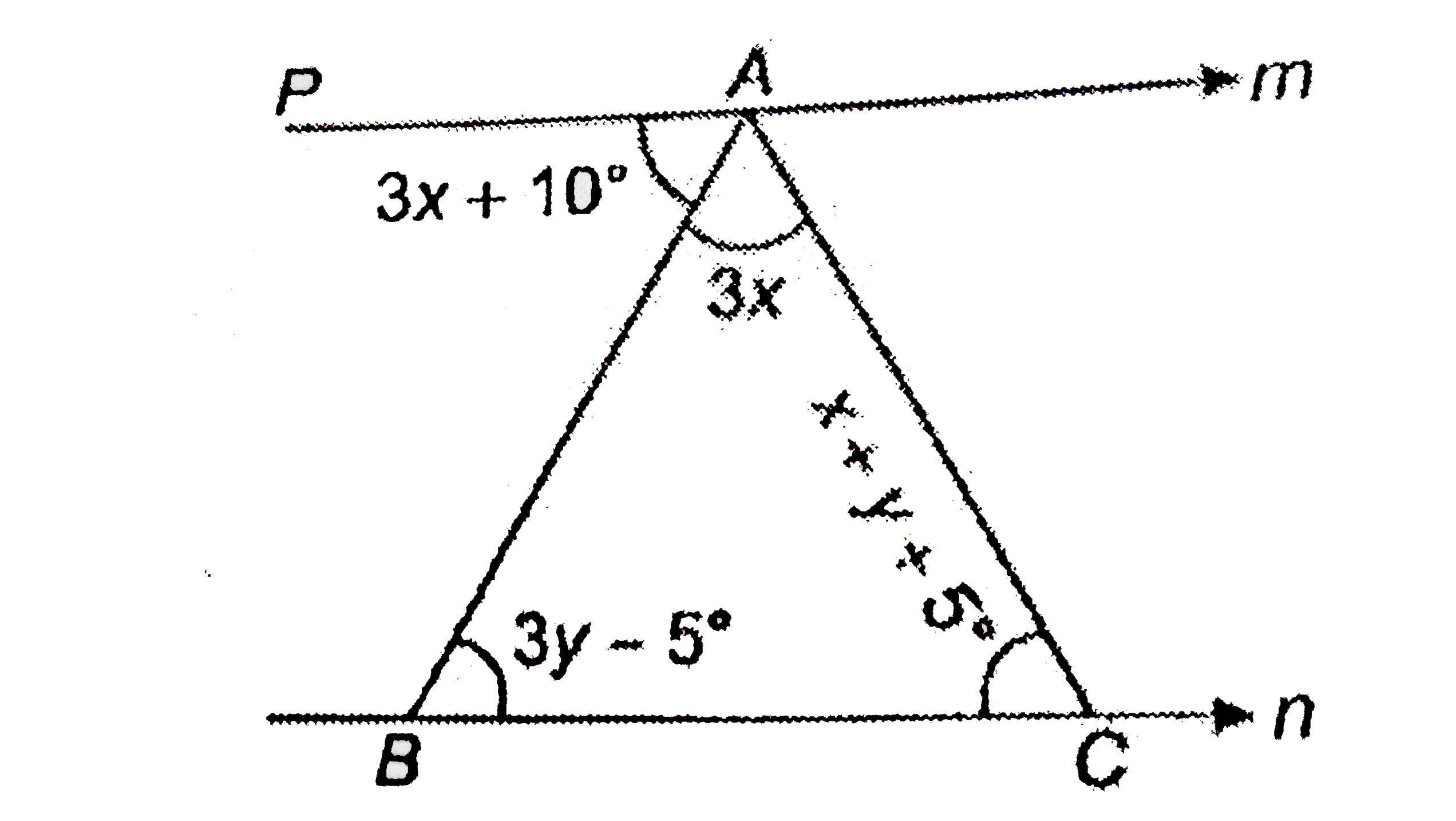 View Solution
View SolutionIn the given figure, ∠DBC=58∘, BD is diameter of the circle. Calculate :
(i) ∠BDC (ii) ∠BEC (iii) ∠BAC
 View Solution
View Solution


