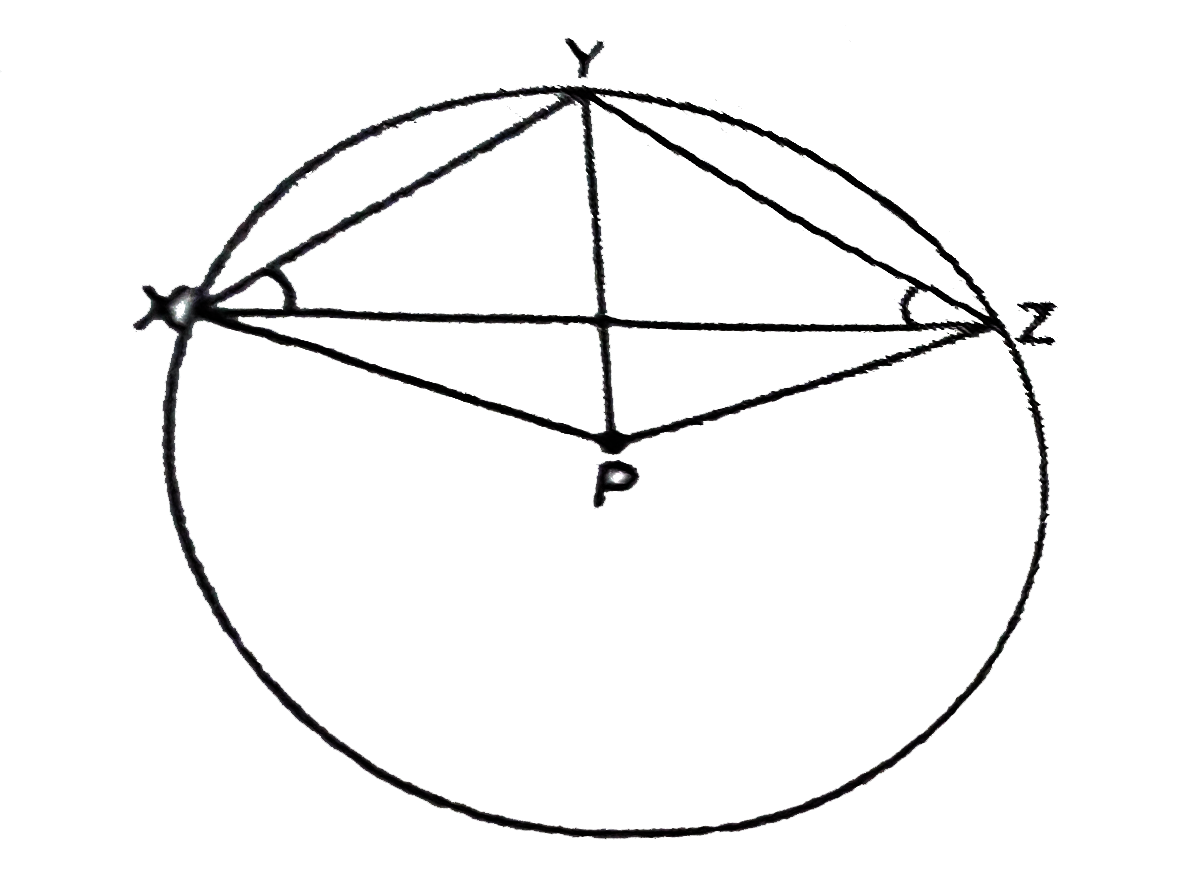
In the figure, P is the centre of the circel. Prove that : ∠XPZ=2(∠XZY+∠YXZ).

Since, arc XY subtends ∠XPY at the centre and ∠XZY at a point Z in the remaining part of the circle.
∴∠XPY=2∠XZY ........(1)
Similarly, arc YZ subtends ∠YPZ at the centre and ∠YXZ at a point X in the remaining part of the circle.
∴∠YPZ=2∠YXZ
Adding eqs. (1) and (2) , we have
∠XPY+∠YPZ=2∠XZY+2∠YXZ
⇒∠XPZ=2(∠XZY+∠YXZ)
Topper's Solved these Questions
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Exercise 10a
Explore 22 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Exercise 10b
Explore 19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (long Answer Question)
Explore 5 Videos
- CO-ORDINATE GEOMETRY Book:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRY Exercise:Exercise
Explore 8 Videos
Similar Questions
In the adjoining figure, P is the centre of the circle. Prove that ∠XPZ=2(∠XZY+∠YXZ).
View SolutionIn the adjoining figure, O is the centre of the circle, Prove that ∠x=∠y+∠z.

View SolutionIn the figure, P is the centre of the circle. Prove that: ∠XPZ=2 (∠XZY+ ∠YXZ)
View SolutionIn figure O is the centre of the circle, prove that ∠z=∠x+∠y.

View SolutionIn Figure, O is the centre of the circle, prove that ∠x=∠y+∠z
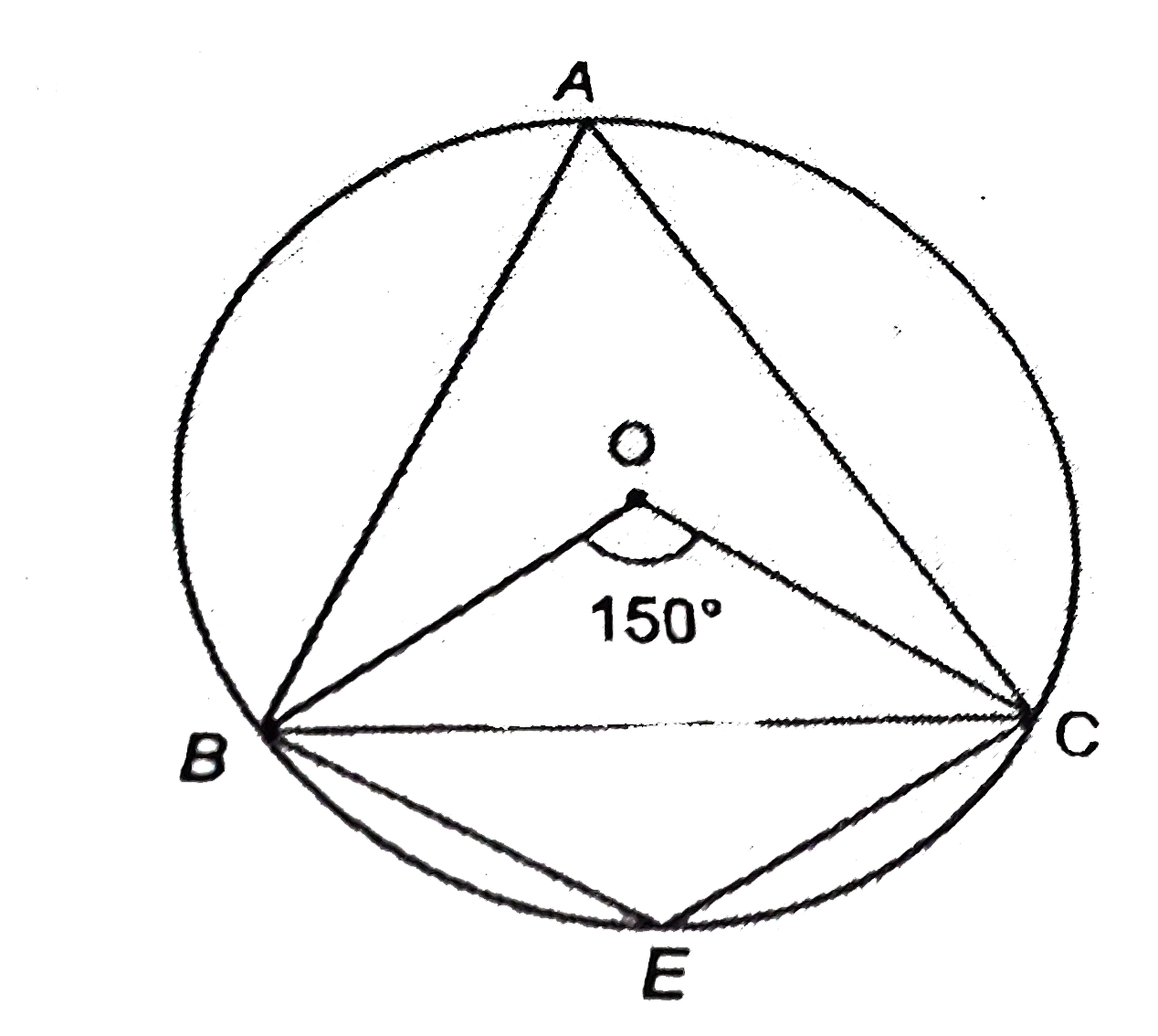
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

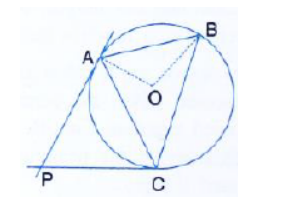
View SolutionIn the given figure, O is the centre of the circumcircle of △ABC. Tangents at A and C intersect at P. Given angle AOB=140∘ and angle APC=80∘ find the angle BAC.
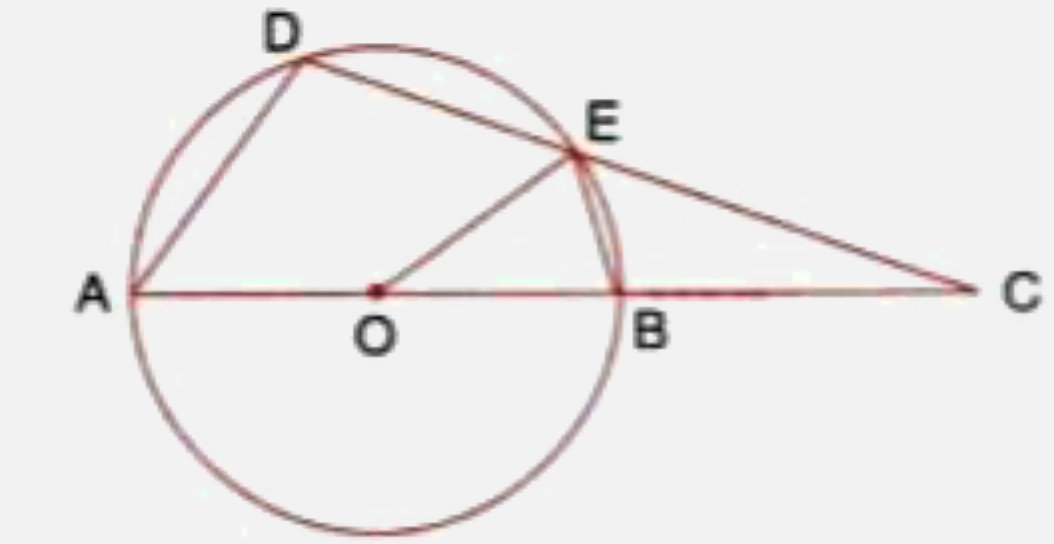
View SolutionIn the figure O is the centre of the circle ∠AOE=150∘,∠DAO=51∘. Calculate the sizes of the angles CEB and OCE.
View SolutionIn Figure, find m ∠PQB where O is the centre of the circle
View Solution

