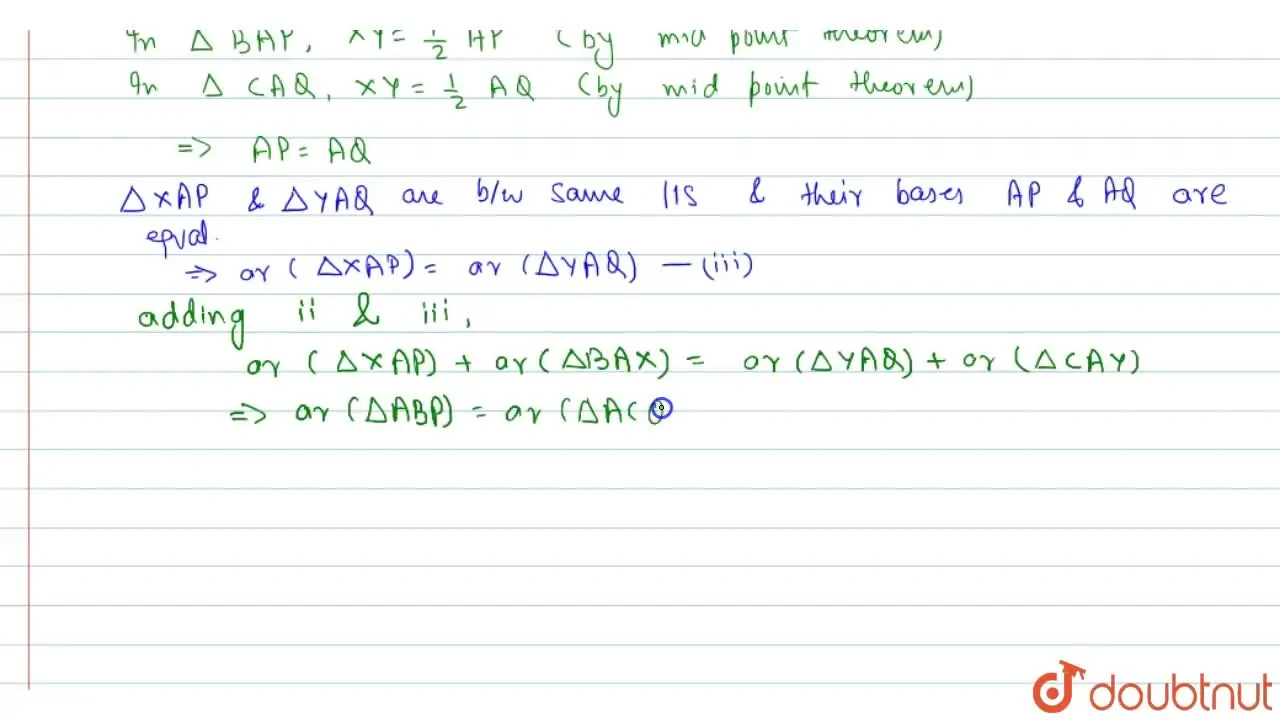In Figure, X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar ( ABP)= ar ( ACQ).
Step by step video & image solution for In Figure, X\ a n d\ Y are the mid-points of A C\ a n d\ A B respectively, Q P || B C\ a n d\ C Y Q\ a n d\ B X P are straight lines. Prove that a r\ (\ A B P)=\ a r\ (\ A C Q). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
In a ABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC intersects FE at Q. Prove that AQ=QP.
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionM, N and P are the mid-points of AB, AC and BC respectively. If MN=3cm, NP=3.5cm and MP=2.5cm , calculate BC, AB and AC
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△PBQ)= ar (△ ARC)
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△RQC)=38 ar (△ ABC).
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△ PRQ)=12ar (△ ARC).
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( △POA)= ar ( △QOC).
View SolutionIn Figure, ∠A=600 and ∠ABC=800, find ∠DPC and ∠BQC
View Solution